长沙理工大学
水利与环境工程学院
港口航道与海岸工程系
《船舶原理》讲稿
课程主讲人:陈龙
2021.9
第一章 船体形状及近似计算
本章要点:
① 船体形状的表示方法,即船舶的特征尺度及船体曲面的图形表示方法;
② 掌握船体近似计算的方法(梯形法、辛氏法、乞贝雪夫法、高斯法)
习 题: 1-1、1-3、1-4、1-5、1-9、1-12
§1-1 主尺度、船形系数和尺度比
船舶形状对船舶性能有很大影响。
船舶的主尺度、船形系数及尺度比是表示船体大小、形状、肥瘦程度的几何参数,这些参数对船舶设计制造、使用和分析性能十分有用。
一、船舶外形表示法
用投影到三个相互垂直的基本平面来表示,称主坐标平面。
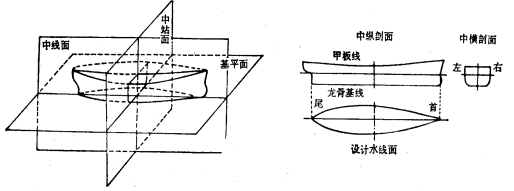
1、中线面:是通过船宽中心的纵向垂直平面,它把船体分成左右相互对称的两部分。(是船体的对称面)
2、中站面:是通过船长中点(垂线间长![]() 、设计水线长
、设计水线长![]() )的横向垂直平面,把船分成首尾两部分。
)的横向垂直平面,把船分成首尾两部分。
3、基平面:能过船长中点龙骨板上缘的平行设计水线面的平面,它与中线面中站面相互垂直。
船体型表面在中线面上的投影是中纵剖面。
船体型表面在中站面上的投影是中横剖面。
船体型表面位于设计水处的平行于基平面的截面称为设计水线面。
二、主尺度 (principal dimension)
主尺度是表示船舶大小的参数,包括船长、型宽、型深和吃水。
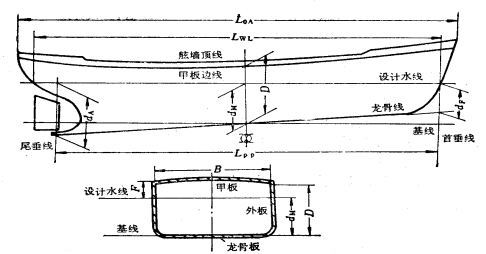
(1)船长[L] Length
船长:总长,垂线间长,设计水线长。
总长![]() (overall):自船首最前端至船尾最后端平行于设计水线的最大水平距离。
(overall):自船首最前端至船尾最后端平行于设计水线的最大水平距离。
垂线间长![]() (perpendiculars):首垂线(F.P.)与尾垂线(A.P.)之间的水平距离。
(perpendiculars):首垂线(F.P.)与尾垂线(A.P.)之间的水平距离。
首垂线:是通过设计水线与首柱前缘的交点可作的垂线(⊥设计水线面)
尾垂线:一般舵柱的后缘,如无舵柱,取舵杆的中心线。军舰:通过尾轮郭和设计水线的交点的垂线。
无特殊说明,船长指垂线间长。
水线长[![]() ](waterline):平行于设计水线面的任一水线面与船体型表面,首尾端交点间的距离。
](waterline):平行于设计水线面的任一水线面与船体型表面,首尾端交点间的距离。
设计水线长:设计水线在首柱前缘和尾柱后缘之间的水平距离。
应用场合:静水力性能计算用:![]()
分析阻力性能用:![]()
船进坞、靠码头或通过船闸时用:![]()
2、型宽[B](breadth moulded)——指船体两侧型表面(不包括船体外板厚度之间垂直于平线面的最大水平距,一般在船长中央处)
对于设计水线处,满载水线处的宽称设计水线宽、满载水线宽。
最大宽度:指包括外板和伸出两舷的永久性固定突出物,如护舷材、舷伸甲板在内,并垂直于中线面的最大水平距离。
3、型深[D](moulded breadth):在甲板边线最低点处,自龙骨板上表面(即龙骨基线),至上甲板边线的垂直距离,通常甲板边线的最低点在中横剖面处。
4、吃水[d](draft):龙骨基线至设计水线的垂直距离。
船前后正常吃水不同,则有首吃水,尾吃水及平均吃水,
无特别说明指平均吃水![]()
![]() ——平均吃水(mean draft),中横剖面处的吃水。
——平均吃水(mean draft),中横剖面处的吃水。
![]() ——尾吃水(after draft),沿尾垂线自设计水线与龙骨线的延长线之间距离。
——尾吃水(after draft),沿尾垂线自设计水线与龙骨线的延长线之间距离。
![]() ——首吃水,沿首垂线自设计水线与龙骨线的延长线之间距离。
——首吃水,沿首垂线自设计水线与龙骨线的延长线之间距离。
5、干舷:[F](freeboard)——自水线至上甲板上表面的垂直距离。
一般船舷首、中、尾所处的干舷是不同的,如无特殊说明,指中横剖面处的干舷F=D-d+t(t——上甲板板的厚度。)
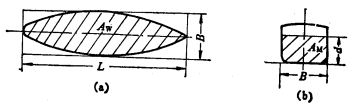
三、船型系数
无因次系数,是表示船体水下部分面积或体积肥瘦程度的无因次系数,它包括水线面系数![]() 、中横剖面系数
、中横剖面系数![]() 、方形系数
、方形系数![]() 、棱形系数
、棱形系数![]() ——纵向棱形系数、垂向棱形系数
——纵向棱形系数、垂向棱形系数![]() 。
。
船型系数对船舶性能影响很大。
(1)水线面系数![]() ——与基平面平行的任一水线面的面积与由船长L、型宽B所构成的长方形面积之比。(waterplane coefficient)
——与基平面平行的任一水线面的面积与由船长L、型宽B所构成的长方形面积之比。(waterplane coefficient)
![]() ,表示是水线面的肥瘦程度。
,表示是水线面的肥瘦程度。
水线面系数与船舶的快速性、稳性有关,客船和军舰的两端较瘦削,其![]() 值也较小,货船油船的两端较丰满,其
值也较小,货船油船的两端较丰满,其![]() 值较大。
值较大。
(2)中横剖面系数[![]() ]——中横剖面在水线以下的面积
]——中横剖面在水线以下的面积![]() 与由型宽B吃水所构成的长方形面积之比。(Midship section coefficient)
与由型宽B吃水所构成的长方形面积之比。(Midship section coefficient)
![]()
中横剖面系数反映中横剖面的饱满程度。通常低速的大型货船的中横剖面比较丰满,其![]() 大而高速的军舰、客船、渔船其
大而高速的军舰、客船、渔船其![]() 值小。
值小。
(3)方形系数[![]() ]——船体水线以下的型排水体积
]——船体水线以下的型排水体积![]() 与由船长L、型宽B、吃水d所构成的长方体体积之比,即
与由船长L、型宽B、吃水d所构成的长方体体积之比,即
![]() (Block coefficient)
(Block coefficient)

![]() 表示的船体水下体积的肥瘦程度,又称排水量系数(displace coefficient)。货船
表示的船体水下体积的肥瘦程度,又称排水量系数(displace coefficient)。货船![]() 较小,客船<货船,军舰最小。
较小,客船<货船,军舰最小。
(4)棱形系数[![]() ]——纵向棱形系数 (prismatic coefficient)
]——纵向棱形系数 (prismatic coefficient)
船体水线以下的型排水体积Δ与相对应的中横剖面面积![]() 、船长L所构成的棱柱体积之比。
、船长L所构成的棱柱体积之比。
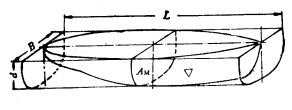
![]()
![]()
![]()
棱形系数表示排水体积沿船长方向的分布情况。与快速性密切相关,高速船![]() 较小,低速船
较小,低速船![]() 较大。
较大。
5、垂向棱形系数[![]() 、
、![]() ]
]
船体水线以下的型体积![]() 与相对应的水线面面积
与相对应的水线面面积![]() ,吃水d可构成的棱柱体积之比。 (Vertical prismatic coefficient)
,吃水d可构成的棱柱体积之比。 (Vertical prismatic coefficient)
即: 
垂向棱形系数表示排水体积沿吃水方向的分布情况。
注:上述系数的定义,如无特殊说明,通常旨设计水线处而言,在计算不同水线处的各系数时,其船长型宽通常用![]() 、
、![]() 。设计水线宽,也可用相对应于各水线处的长宽,但需加以说明,如最大横剖面不在船中处则应取最大横剖面处的有关数据。
。设计水线宽,也可用相对应于各水线处的长宽,但需加以说明,如最大横剖面不在船中处则应取最大横剖面处的有关数据。
四、船型系数的物理意义
船型系数均≤1
![]() :船体水下体积的肥瘦程度
:船体水下体积的肥瘦程度
![]() :船体水下体积的船长分布,或首尾部对于中部的尖瘦或钝肥程度。
:船体水下体积的船长分布,或首尾部对于中部的尖瘦或钝肥程度。
![]() 较小,较多集中在船中部,首尾尖瘦;
较小,较多集中在船中部,首尾尖瘦;![]() 较大,分布较均匀首尾两端丰满。
较大,分布较均匀首尾两端丰满。
![]() :船体水下体积吃水方向分布情况。
:船体水下体积吃水方向分布情况。
![]() 较小,集中在上部,V形剖面;
较小,集中在上部,V形剖面;![]() 较大,分布均匀,U形剖面。
较大,分布均匀,U形剖面。
五、尺度比
尺度比表示船体几何特征的重要参数。
![]() ——长宽比
——长宽比
![]() ——宽度吃水比
——宽度吃水比
![]() ——型深吃水比
——型深吃水比
![]() ——长深比
——长深比
表1-1、1-2各类船舶主尺度比和船型系数的大致范围。
独 立: ![]() 其大小与速航性的好坏有关;
其大小与速航性的好坏有关;
![]() 与稳性、摇荡速航性、操作性有关;
与稳性、摇荡速航性、操作性有关;
![]() 与稳性、抗沉性和船体强度有关;
与稳性、抗沉性和船体强度有关;
可推导出: ![]() 与船体强度和稳性有关;
与船体强度和稳性有关;
![]() 宽深比,与船体强度和稳性有关;
宽深比,与船体强度和稳性有关;
§1-2 船体型线图
船舶外型是一个流线型体,表示其形状最基本的图形是型线图,为了使船舶航行时所受到的阻力最小,船体的表面都做成流线型的光滑曲面,两头尖瘦中间肥大,因此仅用船长、船宽、高三个尺度并不能说明船舶的真实形状和大小,它是通过称为船体外型线图的图样来表示的。
型线图所表示的船体外型为船体型表面。
钢船的型表面为外板的内表面(不包括船体外板硬度)
水泥船、木船则为船壳的外表面(包括船体外板硬度)
以钢质船为例:型线图上所表示的船体形状包括外板型表面的形状和甲板型表面的形状。不包括船壳板和甲板板厚度在内的船体表面(即胁骨以外船壳板以内,横梁以上甲板板以下的船体表面)
采用型表面的原图:
1、各部位钢板的厚度不同。
2、便于建造。
§1-3 船体近似计算方法
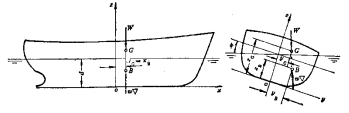
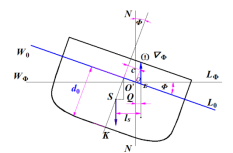
一、船体计算的习惯坐标系
船体计算一般规定如图示为习惯坐标系,
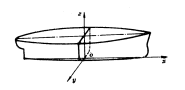 原点 O取在中线面、中站面、基平面的交点,
原点 O取在中线面、中站面、基平面的交点,
中线面与基平面的交线为x轴,x向纵向,指向船首为正;
中站面与基平面的交线为y轴,y向横向,指向右舷为正;
中线面与中站面的交线为z轴,z向垂向,垂直向上为正。
二、近似计算的任务
船厂或设计单位提供的船舶浮性稳性、吃水差、抗沉性和船体强度等资料是根据船体的型线图或各部分重量分布情况、经过大量的计算获得的。
上述计算包括:①船舶重量、重心计算②船体的近似计算。
其中船体近似计算的任务:根据型线图计算出横剖面、水线面的面积以及面积中心的位置,排水体积以及体积的中心、水线面面积惯矩等并据此画出有关曲线和列出有关报告供船员使用,为了正确使用这些资料,需要了解船体近似计算的基本方法和要求。
所有上述船体近似计算,尽量其内容不同,但均可归结为求某条曲线下所围面积。
若某一计算曲线DB,![]() ,积分上下限,曲线所围面积A的定积分式
,积分上下限,曲线所围面积A的定积分式
![]()
船体表面是一个具有双重曲率的复杂表面。
现代科学正在寻求数学表达式,以表示各种船体形状的被积函数,并运用电子计算机,来解决船体计算问题,用数学形式表示的船体型线称为数学型线,有了数学型线,则从船体设计计算到建造施工都可以高度地用自动化。对于一般的船体形状,目前多数还是给出型线图利用型值近似积分法进行船体计算。
由于船舶本身是一个工程建筑物,是一曲流动的音乐。船体在不同受力情况下将产生变形,且由型线图量得的型值存在误差,故船体近似计算的结果允许存在误差,一般其相对误差不超过0.5%是允许的。
船体近似计算方法,主要有梯形法、辛氏法、乞贝雪夫法、高斯法。
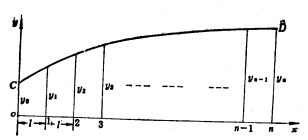
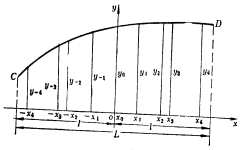
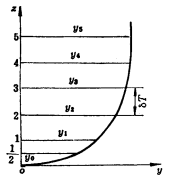
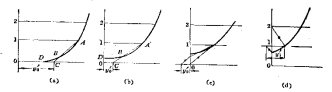
三、梯形法(最简便的数值积分法)
基本原理:用若干直线段组成的折线近似地代替曲线。即:以若干个梯形面积之和代替曲线下的面积。
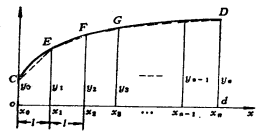
设曲线CD为船体上某段曲线
步骤:将底边![]() 分成间距为
分成间距为![]() 的几等分,过等分点作垂线得
的几等分,过等分点作垂线得![]() 从图中可以看出折线与曲线很接近且随着等分长度的减小而愈加接近。
从图中可以看出折线与曲线很接近且随着等分长度的减小而愈加接近。
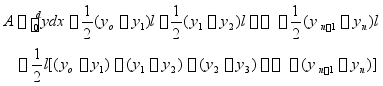
或 ![]()
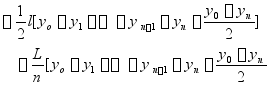 ]
]
式中:L——所求面积积底边的总长;
![]() ——等分间距长;
——等分间距长;
![]() ——等分点之间的距离,其值=
——等分点之间的距离,其值=![]()
简化记忆 ![]()
![]()
具体计算时要列表计算,求总和-修正值
如纵坐标为面积,积分为体积![]() 同理:静矩,惯性矩
同理:静矩,惯性矩
梯形法:简单直观便于变上限积分,在船的性能计算中得到广泛应用。
在船中附近的曲线平直区域梯形面积与计算曲线面积之间的误差很小而在弯曲较明显的首尾区域其误差则较大为降低误差可采取缩短横向坐标间距![]() 的办法(即增加横向坐标的数目)。梯形法的误差与
的办法(即增加横向坐标的数目)。梯形法的误差与![]() 成正比(例题)
成正比(例题)
四、辛氏法
梯形法则假设曲线为折线,若假设计算曲线为抛物线,则称抛物线法,即辛氏法。
基本原理,采用等分间距以若干段二次或三次抛物线近似地代替实际曲线,计算各段抛物线下面积的数值积分法。
船体的大部分曲线事实上是与抛物线相近的。
1. 辛浦生第一法(二次抛物线)

船体上某段曲线CD
原点取在中点o
被积函数

![]() ——
——
令 ![]()
当![]()
![]()
![]() ——
——
= ![]()
![]()
令L为曲线底边长 ![]()
系数[1,4,1]称为辛氏系数
括号前分子为底边长,分母为括号内辛氏乘法之和,即![]() ,所以辛浦生第一法,也称为[1,4,1]法
,所以辛浦生第一法,也称为[1,4,1]法
·应用条件: 曲线底边长度的等分数目为偶数(即纵坐标数目为奇数)
推广:将一个曲线图形的底边分成等间距![]() 的几等分(
的几等分(![]() 为偶数)
为偶数)
纵坐标值![]()
则第0号到第2号纵坐标内的面积是 ![]()
第2~4面积是![]()
依此类推: ![]()
![]()
或![]()
式中:![]() ——等分间距(站距);
——等分间距(站距);
L——底边总长L=![]() ;
;
![]() ——括号内各纵坐标值前辛氏乘数的总和;
——括号内各纵坐标值前辛氏乘数的总和;
A=![]()
辛甫生第一法求面积,同理求体积静矩,惯性矩

具体计算采用表格进行。
2. 辛甫生第二法[1,3,3,1]法
三次抛物线近似地代替实际曲线的辛浦生法。
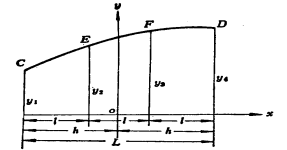
设曲线CD上为船体上的某一段曲线,取等间距的四个坐标![]() 被积函数
被积函数
![]()
![]()
![]() ——
——
取 ![]() ——
——
当![]()
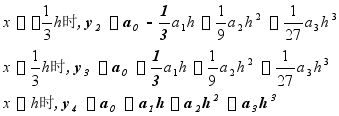
代入式
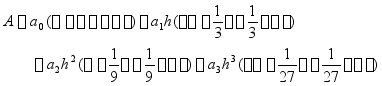 ——③
——③
③=
![]()
令L为曲线底边长L=3![]()
![]()
其中[1,3,3,1]称辛氏乘数 , ![]() 各乘数之和
各乘数之和
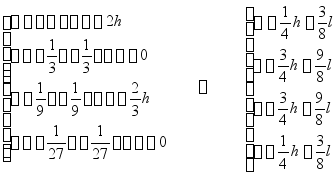
应用条件:适用于将曲线底边长度划分为三等分、六等分、九等分
(即纵坐标数目为4,7,10 …… )
如:六等分 ![]()
![]()
推广:![]() 等分(须为3的倍数)
等分(须为3的倍数)
![]()
采用表格形式计算,适用于体积静矩,惯性矩
3、特殊辛浦生法[5,8,-1]和[3,10,-1]法
[5,8,-1]法:曲线具有两个等分间距,三个纵坐标,但只求曲线下相邻两个纵坐标之间所包围的面积。

推导方法与辛氏一法、辛氏二法一致。
![]()
(5,8两个数字依次用于所求面积的对应的界线坐标)
![]()
![]() 辛氏一法一致
辛氏一法一致
求静矩{3,10,-1}
如求第0号纵坐标和第1号纵坐标之间面积对第0号纵坐标的静矩。
![]()
具体计算[5,8,-1],[3,10,-1]与辛氏一法二法联合起来应用。
4、高次抛物线的辛氏法
抛物线次数 纵坐标法 辛氏系数
2 3 ![]()
3 4 ![]()
4 5 ![]()
5 6 ![]()
6 7 ![]()
高次抛物线的辛氏法,由于辛氏系数复杂,不实用。
辛氏法的误差和间距![]() 成正比
成正比
具体计算见课本例题P14,1,2,3,4
问题梯形法与![]() 成正比;辛氏法与
成正比;辛氏法与![]() 成正比。
成正比。
5、曲线扇形面积及其对![]() 轴、
轴、![]() 轴的静矩的辛氏法。
轴的静矩的辛氏法。
仍然采用数值积分方法
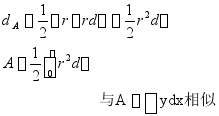
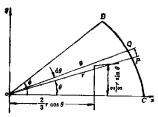
可利用辛甫生法或梯形法
求扇形OCPD的面积重心
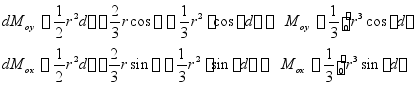
具体计算见例6
五、乞贝雪夫法
梯形法、辛浦生法采用等间距的纵坐标乘上不同的数求加,即求所求曲线下的面积。
乞贝雪夫法基本原理:应用不等间距的各纵坐标值之和,再乘以一个共同的系数来得到曲线下的面积。
用![]() 次抛物线代替实际曲线,采用不等间距的几个纵坐标计算抛物线下的面积。
次抛物线代替实际曲线,采用不等间距的几个纵坐标计算抛物线下的面积。
![]()
乞贝雪夫的各纵坐标对称于原点布置问题各纵坐标距原点的位置;共同系数。
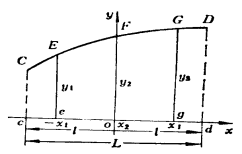
以三个坐标为例的乞贝雪夫法
![]()
三次抛物线方程 ![]()
![]()
![]()
三次抛物线通过E,F,G
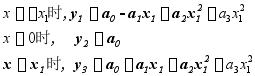
代入式 ![]()
= ![]()
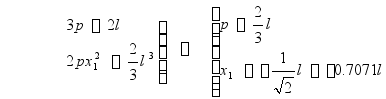
离CD中点![]() 处设立纵坐标
处设立纵坐标
![]()
或 ![]()
为保证精确性采用九个以上纵坐标数
该方法仅用于手算倾角稳性时,船体计算需要绘制乞贝雪夫横剖面图,读取纵坐标值比较繁琐。
六、高斯法
采用不等间距的纵坐标和不同的乘数
![]()
高斯法精确性较高,5个纵坐标的高斯法相当于9个纵坐标的辛氏法或9个纵坐标的乞贝雪夫法。
具体计算见例题7
七、提高船体近似计算精度
1. 增加中间坐标
增加纵坐标的数目,可相应提高精确度,增加工作量选择船长20站,吃水7~9等分,计算结果允许的误差,但首尾末端、舭部曲率变化大,为提高计算的精确度增加中间坐标或编点修正。
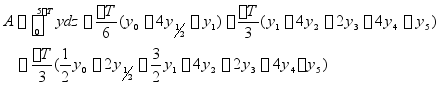
2.端点坐标修正(以半宽水线图为例)
三种情况:
① 船体曲线在端点上,即![]() ,用梯形法计算少算OCA面积
,用梯形法计算少算OCA面积
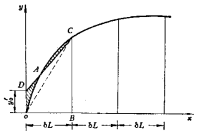
·修正方法:目测法
② 船体曲线超过端点
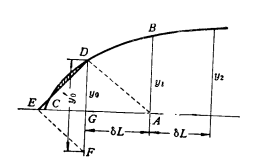
直接按![]() 计算少计算GED面积
计算少计算GED面积
·修正方法:目测法
作直线DE使阴影面积相等
连接AD,过E作EF//AD交DG长线于F ![]() ,即
,即![]()
③船体曲线不到端点,如果![]() 多算SBCE
多算SBCE
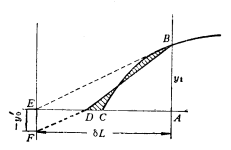
·修正:目测法
证明:未端面积![]()
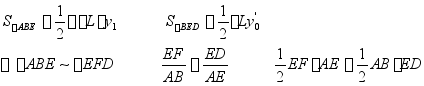
又 ![]()
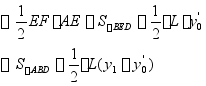
采用-![]()
横剖面端点修正方法同上,但需灵活应用。
计算面积静矩,惯性矩原则上要画出被积函数曲线
问题:端点修正的例题是针对梯形法的,辛氏法是否要端点修正?
积分仪器
面积仪:求水线面横剖面积;
积分仪:是求任何封闭平面图形面积,面积对某一固定轴的静矩或惯性矩;
积分法图仪:绘制任何曲线下面积的积分曲线的仪器。
优点:方法简单、节省时间、提高效率
精确程度取决于仪器本身的精确度,操作人员熟练程度
八、积分曲线特性
船舶静力学计算中,原曲线的积分曲线、重积分曲线之间特性非常重要。
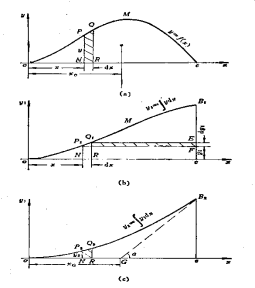
基本特性:
积分曲线在某处的纵坐标值等于原曲线下该处以前的面积,原曲线在某处的纵坐标值为积分曲线在该处的导数,![]() 。
。
积分曲线的极大值或极小值对应于原曲线在![]() 轴上的交点(驻点),原曲线的极大值或极小值对应积分曲线的拐点。
轴上的交点(驻点),原曲线的极大值或极小值对应积分曲线的拐点。
原曲线下的面积对通过C点的纵坐标的静矩等于其积分曲线下的面积或者等于其重积分曲线![]() 所对应的纵坐标。
所对应的纵坐标。
第二章 浮 性
本章要点:船舶在静水中的平衡条件、各种漂浮状态;
船舶在各种浮态下的排水体积、浮心位置的计算原理、方法。
习 题:2-2、2-3、2-7、2-10、2-11、2-14。
§2-1 浮性概述
浮性:船舶在一定的装载情况下,具有漂浮在水面(或浮入在水中)保持平衡位置的能力。
一、船舶平衡条件:
·物体的平衡条件:作用在物体上的两作用力,大小相等,方向相反并作用在同一直线上。
船舶在一定的装载情况下,漂浮于水面一定位置,是一个平衡状态的浮体;
作用在船上的力,有船舶本身的重力以及静水压力所形成的浮力。
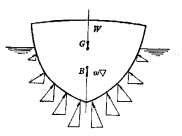
作用在船上的重力是由船舶本身各部分的重量所组成的。如船体构件机电设备,货物人员及行李的重量,军舰还有装备,这些重量形成一个垂直向下的合力,此合力就是船舶重力W,合力的作用点G称船舶重心。
船体浮水表面的每一点都受到水的静压力,方向是垂直于船体面的,其大小与浸水深度成正比,从图中可以看出,船舶水下部分静水压力的水平分力互相抵消,垂直分力则形成一个垂直向上的合力,此合力就是支持船舶漂浮于一定位置的浮力![]() ,合力的作用点B称为船舶的浮心。根据阿基米德定律得物体在水中所受的浮力等于该物体排开水的重量。
,合力的作用点B称为船舶的浮心。根据阿基米德定律得物体在水中所受的浮力等于该物体排开水的重量。
船舶浮力=船舶排开水的重量(排水量)
![]()
![]() ——排水量 t
——排水量 t
![]() ——排水体积 m3
——排水体积 m3
![]() ——重量密度 t/ m3
——重量密度 t/ m3
淡水![]() =1 t/ m3,海水
=1 t/ m3,海水![]() =1.025 t/ m3
=1.025 t/ m3
![]() ——浮力
——浮力 ![]()
浮心B=船舶排水体积![]() 的形心。
的形心。
![]() 综上所述,船舶静止漂浮于一定位置时只受到两个作用力,即作用于重心G并垂直向下的重力W和作用在浮心B垂直向上的浮力
综上所述,船舶静止漂浮于一定位置时只受到两个作用力,即作用于重心G并垂直向下的重力W和作用在浮心B垂直向上的浮力![]() 。
。
船舶平衡条件:(1)重力=浮力 ![]() =
=![]() ;
;
(2)重心G和浮心B在同一条铅垂线上。
讨论平衡问题,要考虑W和![]() 的大小,同时还要注意这些力的作用点位置,采用坐标系,(船体近似计算的常用坐标系)。
的大小,同时还要注意这些力的作用点位置,采用坐标系,(船体近似计算的常用坐标系)。
二、船舶的浮态
船舶浮于静水的平衡状态称为浮态;
船舶的浮态有正浮、横倾、纵倾、横倾+纵倾四种,表示参数、吃水、横倾角![]() ,纵倾角
,纵倾角![]() ;
;
船舶重心位置G(![]() ),浮心B(
),浮心B(![]() )
)
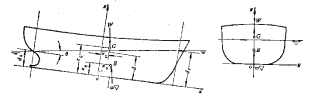
(1) 正浮:船舶漂浮于静水面,船体中纵剖面和中横剖面都垂直于水面的一种浮态,ox,oy轴水平,无横倾和纵倾;
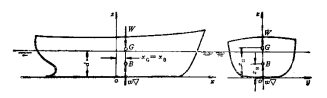

正浮浮态表示参数:吃水 d
(2)横倾状态
船舶自正浮状态向左舷或右舷方向倾斜的一种浮态。ox轴是水平的,中纵剖面与铝垂面成一角度,即正浮时水线面与横倾后的水线面的夹角![]() (横倾角)
(横倾角)
船舶横倾的大小以横倾角表示 有正负:正值,右舷方向横倾;
负值,左舷方向横倾。
浮态表示参数吃水 d ,横倾角 ![]()
(3)纵倾状态
船舶自正浮位置向船尾方向或船首方向倾斜的一种浮态。oy轴是水平的,船体中纵剖面垂直于水面中横剖面与铝垂平面相交成一角度,即正浮时水线面与纵倾后水线面相交的角度![]() “纵倾角”,船舶纵倾大小用首尾吃水差和纵倾角表示。
“纵倾角”,船舶纵倾大小用首尾吃水差和纵倾角表示。
正负:首倾为正值;
尾倾为负值。
浮态表示参数:平衡吃水![]() ,横倾角
,横倾角![]() ,纵倾角
,纵倾角![]()
一般船舶设计或正常使用情况下,都应处于正浮状态或稍有尾倾状态。横倾、大角度纵倾状态和任意状态由于外力作用或船上重量位置的改变或船舶破损后进水等引起,对船舶的使用以及航海性能不利。
从浮态研究船舶浮性问题就是研究船舶稳性问题
都要研究 船舶重力、重心、 浮力、浮心的互相关系
(总布置图) (型线图型值表)
§2-2 船舶重量和重心位置的计算
船舶总重量是船上各类重量之和,已知各项的重量![]() ;
;
![]()
![]() ——各项重量的数目
——各项重量的数目
一、船舶重量分类
1.固定重量:( ![]() )包括船体钢料,木作舾装、机电设备火及武器等,它们的重量在使用过程中是固定不变的,也称空船重量(Light Ship Weight)或船舶自重的重量。
)包括船体钢料,木作舾装、机电设备火及武器等,它们的重量在使用过程中是固定不变的,也称空船重量(Light Ship Weight)或船舶自重的重量。
2. 变动重量:包括货物、船员、行李、旅客、淡水、粮食、燃油、润滑油
以及弹约,这类重量的总和就是船的载重量。
(Displacement Weight)
船舶排水量=空船重量LW+载重量DW
船舶在实际使用中载重量总是变化的,其排水量也随装载情况而变化,固而船舶各种技术性能也发生变化,需用典型的装载情况来反映船舶的各种技术性能。
民船:
空载排水量:是指船舶在全部建成后交船时的排水量,即空船重量,此时动力装置系统内有可供动车用的油和水,但不包括航行时需的燃料,润滑油和炉水储备以及载重量。
满载排水量:指船舶上装载预先规定的设计载重量(即按照设计任务书要求的货物、旅客、船员、行李、粮食、淡水燃料、润滑油、锅炉用水的储备以及备品、供应品等均装载满额的重量)的排水量。
空载排水量、满载排水量又分出港、到港。
出港:燃料、润滑油、淡水、粮食及其他培养物品都按设计的规定的数量带足。 到港:消耗品还利余10%。
满载排水量无特殊说明,指满载出港排水量,是民船的最大排水量,决定船舶的主要要素的出发点,因此也作为民用船舶的设计排水量。
“万吨轮”它的载重量满载时在一万吨上下,
军船:空载排水量
标准排水量
正常排水量
满载排水量
最大排水量
二、空船重量系数和载重系数
空船重量/满载重量=空船重量系数![]() 低值对应于较大的船舶
低值对应于较大的船舶
大型货船0.27~0.36 中小型货船0.30~0.43
总载重量/满载重量=载重系数![]()
显然![]()
大型船舶具有较大的![]() :即它有相对载重较大的特点,这就是船舶向大型化发展和主要原因。
:即它有相对载重较大的特点,这就是船舶向大型化发展和主要原因。
三、船舶重心
1.船舶重心坐标表达式
由于重力是一种平行力系,船舶重心表达式
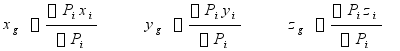
式中:![]() ——船上某一重物的重力;
——船上某一重物的重力;
![]() ——
——![]() 的重心坐标;
的重心坐标;
![]() ——船舶重心的纵向坐标(Longitudinal distance of center of gravity),重心在船中前取正,船中后取负号;
——船舶重心的纵向坐标(Longitudinal distance of center of gravity),重心在船中前取正,船中后取负号;
![]() ——船舶重心的横向坐标(Transverse)坐标;
——船舶重心的横向坐标(Transverse)坐标;
![]() ——船舶重心的垂向坐标(Vertical)坐标。
——船舶重心的垂向坐标(Vertical)坐标。
公式表明:各分力(各重力)对给定平面力矩的代数和等于其合力对该平面之矩,即合力矩定理。
2.空船重心
空船重量![]() 空船重心为
空船重心为![]() 对应坐标(
对应坐标(![]() )
)
![]() 倾斜试验求得,
倾斜试验求得,![]() 根据浮态和
根据浮态和![]() 求得。
求得。![]() 值根据左右重量对称分配的原则应等于零,否则应予以调整。
值根据左右重量对称分配的原则应等于零,否则应予以调整。
3.装卸后重心
根据合力矩原理
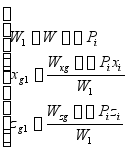
式中:![]() ——装卸前船舶的重量,对应重心坐标
——装卸前船舶的重量,对应重心坐标![]() ;
;
![]() ——所装卸的第
——所装卸的第![]() 项重物的重量,装“+”卸“-”;
项重物的重量,装“+”卸“-”;
![]() ——装卸后船舶重量。
——装卸后船舶重量。
例题:
已知某船![]() ,今天第三货船装货
,今天第三货船装货![]() 试装载后船舶重心的垂向坐标。
试装载后船舶重心的垂向坐标。

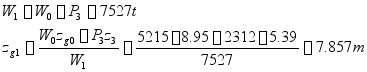
由例题可见,因所装货的重心![]() 低于装货前船舶重心
低于装货前船舶重心![]() 则装货后船舶重心
则装货后船舶重心![]() 将低于
将低于![]() ,反之则
,反之则![]() 高
高![]() 若
若![]() 与
与![]() 同高,则
同高,则![]() 与
与![]() 同高,据此可以控制船舶装货后其重心变化的趋势。
同高,据此可以控制船舶装货后其重心变化的趋势。
上述规律:卸货时相反。
§2—3 排水量和浮心位置的计算
排水体积和排水体积形心坐标的计算是根据型线图和型值表来进行的。
基本内容:在计算船舶的排水体积时,用若干个与任一坐标平面平行的平面把船舶水下体积分割成若干个薄层微体积算出这些薄层微体积,并求其总和,即船舶的排水体积;
计算排水体积形心坐标时,要先算出薄层微体积对某一坐标平面的静矩,并求出这些静矩总和,然后将其总和除以排水体积,即得排水体积的形心距该平面的距离。
计算方法有两种:水下体积沿![]() 轴垂向分割;
轴垂向分割;
水下体积沿![]() 轴纵向分割。
轴纵向分割。
即根据:水线面计算排水体积;
横剖面计算排水体积。
一、根据水线面计算排水体积和浮心位置
1.基本公式
薄层微体积为
![]()
![]() ——离基平面Z处的水线面面积;
——离基平面Z处的水线面面积;
![]()
式中:![]() 是离
是离![]() 轴的
轴的![]() 处的水线面半宽,L是水线长,因L随
处的水线面半宽,L是水线长,因L随![]() 的变化不大,故一般取设计水线长,
的变化不大,故一般取设计水线长,
![]()
该薄层微体积![]() 对平面yoz和xoy的静距
对平面yoz和xoy的静距
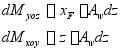
式中![]() 是离基平面Z处的水线面面积的漂心纵向坐标
是离基平面Z处的水线面面积的漂心纵向坐标
(水线面面积的形心F点称为漂心)
求解![]() ,首线水线面面积对
,首线水线面面积对![]() 轴的静矩
轴的静矩
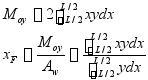
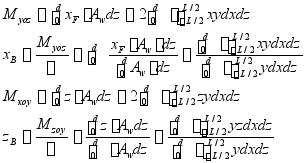
船舶正浮状态时,浮心横坐标![]()
只要改变上限,积分公式成为正变上限积分,按其计算结果便可得到随吃水而变化的关系曲线,如排水体积曲线漂心纵向坐标曲线,浮心垂向坐标曲线,这些曲线与水线面面积曲线漂心纵向坐标曲线,横剖面面积曲线等该称为浮性曲线。
具体计算采用表格
计算排水体积![]() 水线面积及漂心纵向坐标以及随水变化的关系曲线。
水线面积及漂心纵向坐标以及随水变化的关系曲线。
2.水线面计算
包括面积![]() ,漂心纵向坐标
,漂心纵向坐标![]() ,水线面系数
,水线面系数![]() ,图2—8是船舶某一水线面左右舷对称,
,图2—8是船舶某一水线面左右舷对称,![]() 轴放在左舷。
轴放在左舷。
梯形法(20站)
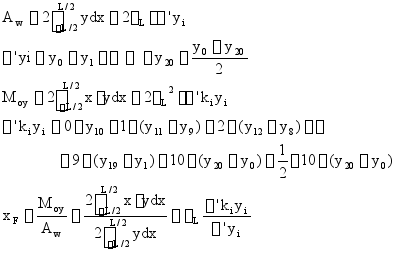
辛甫生法分成10等分![]() ,首尾变化曲率大,增加中间坐标
,首尾变化曲率大,增加中间坐标

例题P42,梯形法,辛甫生法
3.水线面面积曲线
根据前面分别计算出船舶在各个吃水处的水线面面积,然后以各个吃水处的水线面面积为横坐标,以吃水为纵坐标,绘制出水线面面积和吃水的关系曲线,此曲线称水线面面积曲线![]()
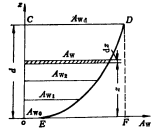
特性: ![]()
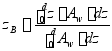
面积形心的垂向坐标=浮心垂向坐标![]()
![]()
水线面面积曲线的形状反映排水体积沿吃水方向的分布情况。
4.每厘米吃水吨数曲线
船舶吃水平行于水线面增加(或减小)1cm时引起排水量增加(或减小)的吨数称每厘米吃水吨数。
根据水线面面积曲线可以得出在任何吃水时的每厘米吃水吨数。
设船舶在吃水d时,水线面面积![]()
吃水改变![]() 时,排水体积变化是
时,排水体积变化是![]()
排水量变化![]()
![]() ——水的重量密度
——水的重量密度![]()
当![]()
![]() (
(![]() )
)
TPC每厘米吃水吨数,只与![]() 有关(
有关(![]() 常数)
常数)
由于![]() 随
随![]() 变化而变化,固此TPC也将随吃水不同而异,将TPC随吃水的变化绘制成曲线
变化而变化,固此TPC也将随吃水不同而异,将TPC随吃水的变化绘制成曲线![]() ,称为每厘米吃水吨数曲线,该曲线的形状与水线面面积曲线完全相似。
,称为每厘米吃水吨数曲线,该曲线的形状与水线面面积曲线完全相似。
应用:已知船舶TPC曲线便可查出吃水d时的TPC数值,能迅速求出卸小量货物![]() (不超过排水量10%)以后的平均吃水变化量
(不超过排水量10%)以后的平均吃水变化量![]() ,
,
超过10%排水量不适用,因吃水变化较大,TPC就不能看成常数,通常利用排水量曲线求解。
5.排水体积曲线

计算并绘制排水体积随吃水变化的关系曲线此曲线称为排水体积曲线。
根据水线面面积曲线,利用梯形法求排水体积。
P46 例表2—4 未端点修正
根据计算结果以吃水为纵坐标,排水体积为横坐标,图形在船底水线处成微曲向上近似一条倾斜直线。
排水体积曲线包括型排水体积![]() 曲线;总排水体积
曲线;总排水体积![]() 曲线
曲线
★![]() 值是根据型线图计算所得,称型排水体积(不包括船壳板附体)(舭龙骨、舵支轴架、螺旋桨)
值是根据型线图计算所得,称型排水体积(不包括船壳板附体)(舭龙骨、舵支轴架、螺旋桨)
★包括附体的体积为总排水体积![]()
![]() 小船取大值;大船取小值
小船取大值;大船取小值
船壳系数1.006
排水量![]()
排水体积曲线是水线面面积曲线的积分曲线。
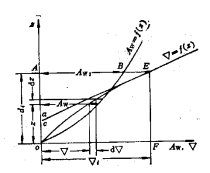
特性![]()
![]() 对基平面静矩
对基平面静矩 ![]()
又![]() =面积OEF
=面积OEF
浮心垂向坐标![]()
排水体积曲线和![]() 轴可的面积OAE属于排水体积
轴可的面积OAE属于排水体积![]() 对吃水
对吃水![]() 的水平面的静矩。
的水平面的静矩。
面积![]()
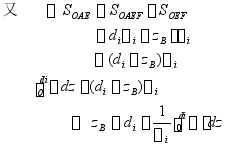
通过排水体积曲线上任一点E的切线与![]() 轴的夹角的正切等于该点处
轴的夹角的正切等于该点处![]() 。
。
理论:

校核排水体积曲线和水线面面积曲线的计算结果。
![]()
6.浮心坐标曲线
船舶浮心即排水体积的形心,其位置可由纵向,横向,垂向坐标确定。
一般船舶水下部分左右舷对称![]()
浮心位置随吃水变化的关系曲线分别为浮心纵向坐标曲线![]() 和浮心垂向坐标
和浮心垂向坐标![]()
船舶在某一固定吃水时,浮心纵向坐标![]() 和垂向坐标
和垂向坐标![]() 可按前面已得出的公式进行计算。
可按前面已得出的公式进行计算。
任意吃水![]() 浮心坐标的计算系用变上限积分公式。
浮心坐标的计算系用变上限积分公式。
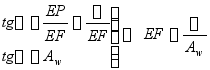
(1) 浮心纵向坐标
不同吃水处漂心的纵向坐标,绘制![]() 曲线
曲线
变上限积分:计算方法和变吃水情况下排水体积曲线的计算相类似。
梯形法列表计算P49表2—5
根据结果绘制浮心的纵向坐标曲线
特点:
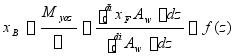
对吃水Z求导数
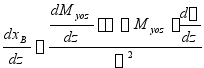
![]()
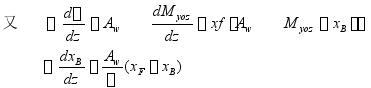
叙述如下:
吃水d时,水线![]() ,增加微量
,增加微量![]() 水线为
水线为![]() ,增量
,增量![]() ,形心的坐标
,形心的坐标![]() ,
,![]()
对B取矩![]()
![]() 高阶微量:
高阶微量:![]()
当![]()
若漂心的纵向坐标![]() 和浮心的纵向坐标曲线是按同一比例给出的,则在曲线
和浮心的纵向坐标曲线是按同一比例给出的,则在曲线![]() 与
与![]() 相交处(
相交处(![]() )
)
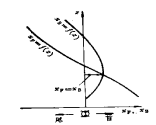
曲线![]() 有最大值或最小值(图示为最大值)
有最大值或最小值(图示为最大值)
此特性可绘制浮心纵向坐标和校验其计算结果。
例题表(2—6)P50
(2) 浮心垂向坐标曲线
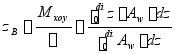 根据水线面面积曲线计算
根据水线面面积曲线计算
![]()
![]()
实际原理清晰进行变上限积分
但采用数值积分法计算得到的排水体积对基平面的静矩,偏大![]() 偏高。
偏高。
因此,通常按照计算,绘制浮心垂向坐标。

从式中知![]() 吃水增加,浮心升高
吃水增加,浮心升高
所以船舶的浮心垂向坐标曲线![]() 是随吃水增加而增长的。
是随吃水增加而增长的。
例题,表2—8、2—9
二、 根据横剖面沿船长方向积分,计算体积和浮心位置。
纵向计算法
1. 基本公式
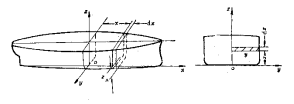
船舶在吃水d时的正浮状态
在离中站面![]() 处,取
处,取![]() 薄层进行分析
薄层进行分析
![]()
![]()
(![]() 是离
是离![]() 轴
轴![]() 处的水线面半宽)
处的水线面半宽)
![]()

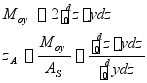

船舶正浮状态,浮心横向坐标![]()
2.横剖面计算
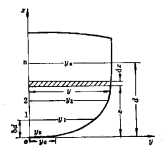
内容包括:横剖面面积![]() ,面积形心垂向坐标
,面积形心垂向坐标![]()
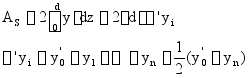
![]() —— 端点修正后的半宽值;
—— 端点修正后的半宽值;
![]() ——各水线等间距值。
——各水线等间距值。
横列面面积对![]() 轴的静矩
轴的静矩
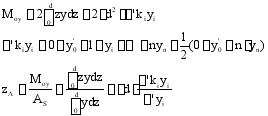
中横剖面系数![]()
![]() ——中横剖面积;
——中横剖面积;
![]() ——中横剖面船宽
——中横剖面船宽
例题梯形法P55,表2—10
辛甫生法
舭部曲线变化较大增加中间坐标以提高精确度,减小误差。
计算如表2—11
3.排水体积和浮心坐标
按照横剖面计算方法![]() 对基平面的静矩
对基平面的静矩![]() 和面积
和面积![]() 形心垂向坐标
形心垂向坐标![]() 计算出来——数值积分法(梯形法)。
计算出来——数值积分法(梯形法)。
P56表2—12
4.横剖面面积曲线
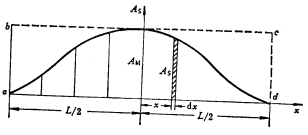
(1)![]()
![]()
(2)
(3)![]()
反映了船舶排水体积沿船长的分布情况
上述特性重要:根据船舶的任一水线下的横剖面面积曲线可以较方便地求出该水线下的排水体积和浮心纵向坐标也是设计新船型线图的主要根据之一。
结论:两种方法结果相同,相互补充以便校核。
第一种方法:求船舶正浮状态下随吃水变化的排水体操作,和浮心坐标。
第二种方法:在船舶使用过程中,由于载荷变化,破损进水火及可浸长度下水计算等,涉及到船舶在纵倾状态下的排水体积和浮心坐标或者计算船体强度,需要画浮力曲线图。
§2—4 船舶在纵倾状态下排水体积和浮心坐标的计算
船舶在正浮状态下的排水体积和浮心位置的计算方法,船舶在营运中通常存在一定得纵倾,当纵倾不大时,可用平均吃水作为正浮吃水,查排水量曲线求得排水量,当纵倾较大时或在波面水线时需Bonjean Curves,但在船舶设计建造过程中,经常需要知道船舶在纵倾状态下的排水量和浮心位置,利用邦戎曲线或费尔索夫图谱求出。
一、邦戎曲线

![]() 曲线
曲线
不同吃水横剖面面积变化限积分
![]()
以吃水 d为纵坐标,横剖面面积![]() 为横坐标
为横坐标
绘制出 ![]()
将型线图上各站处的横剖面都进行如上的计算,各横剖面在不同吃水下的面积![]() 一组曲线邦戎曲线Bonjean
一组曲线邦戎曲线Bonjean
为便于计算船舶在作倾水线下的浮心及各舱形心的垂向坐标,在邦戎曲线图上,还画出横剖面对基平面的静矩曲线,具体计算分成三部分最高等分水线火下部分;最高等分水线甲板边线部分;甲板边线梁拱部分。
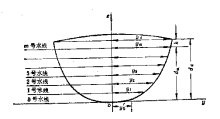
(1)![]()
![]()
![]()
式中:![]() ——横剖面在等分水线自制半宽;
——横剖面在等分水线自制半宽;
![]() ——等分水线的等分间距。
——等分水线的等分间距。
�������� 端点进行修正
(2)![]() 梯形
梯形
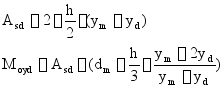
(3)![]()
梁拱是二次抛物线
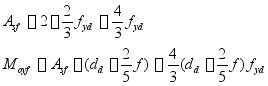
![]() ——
——![]() 的形心距底边的高度;
的形心距底边的高度;
梁拱![]() 在各站处横剖面上的数值是不同的
在各站处横剖面上的数值是不同的
因为全船的甲板梁拱线是同一抛物线的一部分
在甲板最宽处的梁拱最大随着甲板宽度减少,梁拱也随着减小至船首尾端为0。
梁拱求解方法计算
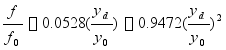
船舶型宽处的半宽值![]()
![]() 船舶型宽设计给定的梁拱高度
船舶型宽设计给定的梁拱高度
![]() 计算横剖面的甲板边线半宽值
计算横剖面的甲板边线半宽值
查表梁拱值曲线图P60,图2-24
![]() 某一站号处
某一站号处 ![]()
![]()
另:横剖面在各水线下的面积对基平面的静矩![]() 亦可以用各站号处的面积曲线
亦可以用各站号处的面积曲线![]() 求得
求得
因为横剖面面积曲线![]() 是横剖线的积分曲线
是横剖线的积分曲线
此面积曲线与基线![]() 轴之间的面积即表示横剖面对基平面的静矩
轴之间的面积即表示横剖面对基平面的静矩
为了缩短图纸的长度和使用方便起见,绘制邦戌曲线图
对船长和型深采用不同的比例尺,一般型深方向的比例常比船长方向的比例为大,绘出的船弄显得短而高。
注意:计算时一直要计算到甲板。
邦戎曲线:算出任意纵倾水线下(亦包括正浮状态)的排水体积和浮心位置。
步骤如下:P60 (1)(2)(3)(4)。交点作平行基线的直线
稳性计算,舱容计算,可浸长度计算,下水计算,船体总强度计算
二、费尔索夫图谱(略)
§2-6在水的重量密度改变时船舶浮态变化
船舶航行于各个港口,当各个港口水的密度不同时,必将引起船舶吃水的变化,例如上海是淡水港,其水的密度约为1.010![]() ,大连是海水港,其水的密度约为1.025
,大连是海水港,其水的密度约为1.025![]() ,当船舶自大连驶入淡水(上海)时,其吃水差是多少?
,当船舶自大连驶入淡水(上海)时,其吃水差是多少?
1. 吃水变化
![]() 对水的重量密度微分排水量不变
对水的重量密度微分排水量不变
![]()
![]()
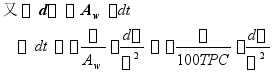
淡水![]() 海水
海水 ![]() 吃水减小
吃水减小
海水![]() 淡水
淡水 ![]() 吃水增加
吃水增加
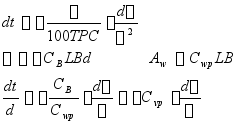
![]() 垂向棱形系数
垂向棱形系数 ![]() 原来液体的重量密度
原来液体的重量密度
![]() 吃水减小2%
吃水减小2%
2. 浮心位置变化
淡水![]() 海水,海水
海水,海水![]() 淡水 ,吃水发生变化,排水体积也发生变化,使浮心位置随之变化
淡水 ,吃水发生变化,排水体积也发生变化,使浮心位置随之变化
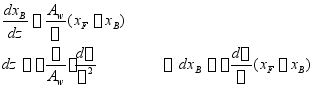
同理:![]()
讨论:对大多数船舶而言![]() 小于
小于![]() ,即
,即![]()
淡水![]() 海水,
海水,![]() 浮心向船首移动
浮心向船首移动
同时船舶的重量都没有改变,浮心和重心不在同一条铝垂线上,便形成纵倾力矩,使船舶发生尾倾
海水![]() 淡水,使船舶发生首倾
淡水,使船舶发生首倾
![]() 浮心,漂心在同一铅垂线上,
浮心,漂心在同一铅垂线上,![]() 改变对纵倾无影响
改变对纵倾无影响
![]() 淡水
淡水![]() 海水,
海水,![]() 浮心向下移动
浮心向下移动
海水![]() 淡水,
淡水,![]() 浮心向上移动
浮心向上移动
3. 等重条件:
淡水![]() 海水,海水
海水,海水![]() 淡水,船舶重量W不变
淡水,船舶重量W不变
![]()
W——船舶重量
4. 吃水改变量
(1)等重
![]()
排水体积改变量:![]()
吃水改变量: ![]()
若:海水![]() 淡水 或 淡水
淡水 或 淡水![]() 海水,为平行沉浮,考虑到吃水改变量
海水,为平行沉浮,考虑到吃水改变量![]() 的数值不大,故海水中水线面积
的数值不大,故海水中水线面积![]() 与淡水中的水线面积
与淡水中的水线面积![]() 可近似看相当
可近似看相当
排水体积变化量:![]()
![]()
![]()
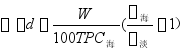
TPC海——吃水d时的每厘米吃水吨数
例题:已知某船重量W=18000 t在海水中的吃水![]()
![]() 已知上海港淡水密度
已知上海港淡水密度![]() 求该船驶入上海港后的吃水。
求该船驶入上海港后的吃水。
解:![]()
淡水吃水,![]()
(2)变重和平行沉浮
事实上船舶由海(淡)入淡(海)过程中,在油水消耗及打入抽出压载水等重量变化 的情况下,作两步处理
在等重条件下,![]() ;
;
根据装卸重物![]() 位于漂心垂线上,曲式
位于漂心垂线上,曲式![]() 求出装卸引起的吃水改变量。
求出装卸引起的吃水改变量。
(3)近似计算公式
精确公式计算繁琐,驾驶员用计算公式![]()
例题:![]()
比较结果,增大2cm
![]()
![]()
![]()

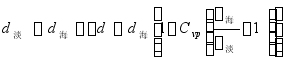
当 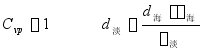
![]() 随船舶类型变化
随船舶类型变化
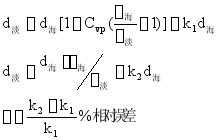
说明:![]() 愈小其相对误差越小;
愈小其相对误差越小;
淡水密度越大相对![]() 越小;
越小;
海水![]() 淡水,近似计算
淡水,近似计算![]() 值偏大即偏于安全对经营经济而言则意味着少装一定量的货。
值偏大即偏于安全对经营经济而言则意味着少装一定量的货。
§2-7 储备浮力与载重线标志
一、 浮性衡准
船舶实际重量![]() 船舶装载重量
船舶装载重量![]() (fall load weight)或船舶实际吃水
(fall load weight)或船舶实际吃水![]() 满载吃水
满载吃水![]() (fall load draft)
(fall load draft)
![]() 船舶浮性衡准是通过限定吃水来加以实现,如果船舶超载致使实际吃水超过满载吃水,则港务机关根据“载重线公约”有权不准船舶离港。
船舶浮性衡准是通过限定吃水来加以实现,如果船舶超载致使实际吃水超过满载吃水,则港务机关根据“载重线公约”有权不准船舶离港。
二、 储备浮力
船舶在水面的漂浮能力是由储备浮力来保证的。
由于船舶漂浮在水面,必须具备浮力二重力的平衡条件,当船舶在波浪中或冰区航行时,难免甲板上浪或结冰,这就等于增加了船舶的载荷,为了保证船舶和船员的安全,需要在满载水线上储备一定的水密船体容积,以适应甲板上浪或结冰所增加临时性载荷的需要上述水线以上水密船体容积所具有的浮力称为储备浮力。
由此可见,为保证船舶的浮性,必须具备一定的储备浮力。
(Reserve buoyanly)其他航海性能亦需要一定的储备浮力储备浮力的大小与船舶的大小、类型、航行季节和航区周围有关海船的佬备浮力约为其满载重量的25.40%内河船均为10~15%油船固本身特点其储备浮力要比一般于货船小。
海面的风浪冬季比夏季大要求冬季有较大的储备浮力为了保证船舶具有一定的储备浮力,就不允许船舶超载,而具体的是通过勘定满载吃水来实现。
![]()
![]() ——计算型深(型深+干舷甲板边板的厚度);
——计算型深(型深+干舷甲板边板的厚度);
F——勘定的干舷高度。
三、 干舷高度的勘定
“国际船舶载重线公约”海载
![]()
式中:![]() :夏季最小干舷高度
:夏季最小干舷高度
![]() :基本干舷,由船长确定
:基本干舷,由船长确定
![]() ——由
——由![]() ,上层建筑围壁情况和船舷等因素确定修正值。
,上层建筑围壁情况和船舷等因素确定修正值。
![]() ——由季节,航区以及舷外水密度确定的修正值
——由季节,航区以及舷外水密度确定的修正值
确定F的基本精神:是船舶除平衡满载重量WF的浮力外必须保证具有满载重量的一定百分数的储备浮力的安全载重线标志。
第三章 初稳性
本章要点:1,初稳性概念,初稳性高度,初稳性公式、船舶稳性指标及判断方法。
2,静水力曲线计算及绘图。
3,载荷的移动和装卸,自由液面等对船舶浮态及初稳性跟影响。
4,船舶倾斜试验目的及原理。
作业题: 3-3,3-4,3-7,3-9,3-12,3-14,3-17
§3-1 概述
一、稳性概念
![]() 船舶在外力作用下偏离其平衡位置而倾斜,当外力消失后,能自行回复到原来平衡位置的能力。
船舶在外力作用下偏离其平衡位置而倾斜,当外力消失后,能自行回复到原来平衡位置的能力。
船舶静止漂浮于水面某一位置时,受到两个作用力,其大小相等方向相反,而且两个力的作用点在同一垂直线上,船舶处于平衡位置。但经常受到风浪等各种外力的作用,使其发生倾斜,破坏原来平衡时的平衡状态。
船受外力作用发生倾斜,船的重量倾斜前后没有改变,故排水体积大小没有发生变化;但水线位置的变化使水下体积的形状已经改变,浮心位置发生改变,形成复原力臂GZ。
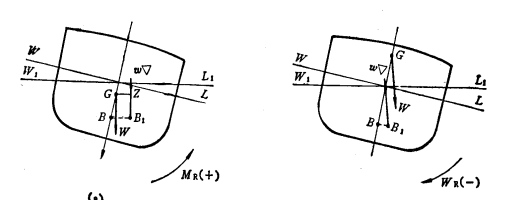

M![]() =
=![]() ·
·![]()
![]()
复原力矩与倾斜力矩方向相反,起到抵抗倾斜力矩的作用,MR定为正值。
倾斜力矩大小取决于?风、浪、船上货物的移动,旅客的移动,外界以及船舶的回转;复原力矩大小取决于?排水量,重心高度及浮心移动的距离等。
方向相同,不仅起不到抵抗倾斜的作用,反而促使舰艇继续倾斜。
浮态{ 横倾(向左舷或右舷侧的倾斜)横倾力矩:倾斜力矩的作用平面平行于中横剖面时产生横倾。纵倾(向首或船尾的倾斜)。纵倾力距在中纵剖面产生纵倾。
![]() 概念: 静稳性:假若倾斜力矩的作用是从零开始逐渐增加,使船舶倾斜时的角速度根据力的作用方式、速度,很小,可忽略不计
概念: 静稳性:假若倾斜力矩的作用是从零开始逐渐增加,使船舶倾斜时的角速度根据力的作用方式、速度,很小,可忽略不计
动稳性:突然作用在船舶上,初始值即不为零,使船舶倾斜时有明显的角速度变化。
造成船舶离开平衡位置的是倾斜力矩,产生的原因有:风浪的作用、船上货物的移动力、旅客集中于单一船舷、拖船的急牵、火炮的发射等。
复原力矩的大小取决于排水量,重心和浮心的相对位置等因素。
M![]() =
=![]() ·
·![]()
经过以上的分析,我们对稳性进行下列两部分讨论:
根据角度:(1)初稳性(或称小倾角稳性)——指倾斜角度小于10度~15度或上甲板边缘开始入水前的稳性。
(2)大倾角稳性——一般指倾角大于10度~15度或上甲极边缘开始入水后的稳性。
划分原因:小倾角稳性可引入某些假定,既使浮态计算被简化,能获得稳性的各种因素之间的规律。
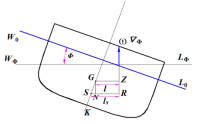
§3-2 浮心的移动、稳心及稳心定律
讨论稳心问题,首先(1)需要确定倾斜水线的位置。
在利用符拉索夫曲线计算在纵倾状态、横倾状态下排水体积和浮心坐标时倾斜水线也是满足一定条件下才得以计算。
(2)其次找出浮力作用线的位置。(3)确定复原力矩的大小及方向。
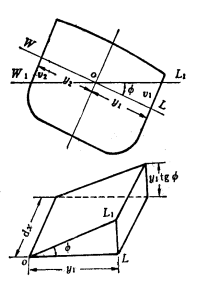 一、等体积倾斜水线
一、等体积倾斜水线
船体受倾斜力矩排水体积保持不变,W1L1是等体积倾斜水线。
S![]() =
=![]()
![]()
![]() 沿船长取一微段:dx dv
沿船长取一微段:dx dv![]() =
=![]()
整个入水楔形的体积:
![]()
![]()
同理,整个出水楔形的体积: ![]()
在等体积倾斜时 V![]() =V
=V![]()
![]()
而积分 ![]() 及
及![]() 分别表示水线面WL在轴线o—o两侧的面积对轴线o—o的静矩。
分别表示水线面WL在轴线o—o两侧的面积对轴线o—o的静矩。![]() 水线面WL对于轴线o—o的面积静矩为0,亦即o—o通过水线面WL的形心漂心。
水线面WL对于轴线o—o的面积静矩为0,亦即o—o通过水线面WL的形心漂心。
结论:两等体积水线面的交线o—o必须通过原水线面WL的漂心。
![]() 已知船的倾角
已知船的倾角![]() (小角度)及原水线WL的漂心位置,即可确定等体积水线W1L1的位置。一般船舶分舷对称。
(小角度)及原水线WL的漂心位置,即可确定等体积水线W1L1的位置。一般船舶分舷对称。
注:结论可适合纵倾情况。
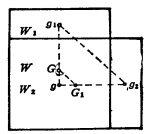
二、浮心的移动
浮心的移动是借助重心移动原理 ![]() //
//![]()
 =
=![]() 或
或![]()
 该式表明,整个重心的移动方向平行于局部重心的移动方向且重心移动的距离
该式表明,整个重心的移动方向平行于局部重心的移动方向且重心移动的距离 ![]() 与总重量W成反比。
与总重量W成反比。
现在研究浮心的移动距离 ![]() 且
且![]() ,由于
,由于![]()
![]()
![]() 其中
其中![]() 是体积对o—o轴的静矩
是体积对o—o轴的静矩
![]()
在![]() 为微小角度时
为微小角度时![]() ,故
,故 ![]()
其中积分式![]() 是水线面WL的面积对纵向中心轴线o—o的横向惯性矩
是水线面WL的面积对纵向中心轴线o—o的横向惯性矩![]() ,
,![]()
![]() (与
(与![]() 成正比,与
成正比,与![]() 成反比) {讲授如何计算
成反比) {讲授如何计算![]() (
(![]() )}
)}
三、稳心及稳心半径 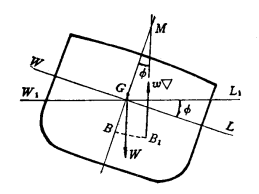
船舶在横倾![]() 角后,浮心自原来的B点沿某一曲线移到B1点,此时浮力的作用线垂直于W1L1,并于中线相交于M点。当
角后,浮心自原来的B点沿某一曲线移到B1点,此时浮力的作用线垂直于W1L1,并于中线相交于M点。当![]() 角度很小
角度很小 ![]() 可看作圆弧的一段,M点为圆心,
可看作圆弧的一段,M点为圆心,![]() =
=![]() 为曲线半径。这样船舶在微小角度倾斜过程中,浮力作用线均通过M点,
为曲线半径。这样船舶在微小角度倾斜过程中,浮力作用线均通过M点,![]() M点称为横稳心或初稳心。
M点称为横稳心或初稳心。![]() 称为横稳心半径或初稳心半径。
称为横稳心半径或初稳心半径。
![]() 当
当![]() 微小角度
微小角度 ![]() 代入
代入![]()
![]()
即:假定船舶在等体积小角度倾斜过程中,浮心移动曲线是以稳心半径为半径的圆孤,稳心M点保持不变,实际解决问题可推广到10度~15度的初稳性的情况。浮力作用线通过稳心M。
同理,等体积纵倾情况的稳心半径
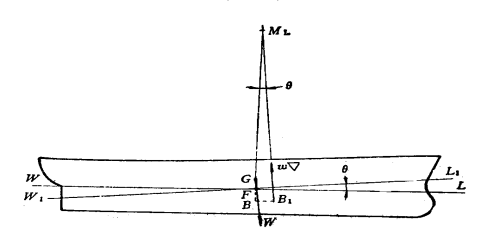

(1)等体积倾斜水线面![]() 与WL相交于通过漂心横向轴线。
与WL相交于通过漂心横向轴线。
(2)浮心的移动距离为 ![]()
![]()
![]() 水线面面积对于通过漂心的横向轴的纵向惯性矩。
水线面面积对于通过漂心的横向轴的纵向惯性矩。
(3)纵稳心半径![]()
(讲授如何计算![]() ,
,![]()
![]() )
)
水线面面积对船中横轴的纵性惯性矩 I=2![]()
![]() ——水线面积
——水线面积
![]() ——漂心纵向坐标
——漂心纵向坐标
计算:![]()
![]() 、
、![]() 、→
、→![]() 、
、![]()
根据型线图型值表: ![]()
梯形法 ![]()
![]()
![]()
I——水线而对过船中的模轴的纵向惯性矩
![]() ——水线面的漂心纵向生标
——水线面的漂心纵向生标
数值积分 ![]()
![]()
梯形法 ![]()
![]()
数值积分的表达式、表格计算详见本章附表。
提问:
1、根据倾斜角度船舶稳性可分为初稳性(小倾角稳性)和大倾角稳定为什么要这样分?
答:可以引入某些假定,使浮态计算简化,能够较明确获得影响初稳性因素之间的规律。
2、浮心移动公式计算表达用了什么原理?
答:重心移动原理。
§3-3 初稳性公式,稳性高
一、稳性分类
(1)按作用力矩性质分静稳性和动稳性。
静稳性:船舶在倾斜过程中不计及角加速度和惯性矩的稳性,它研究倾斜力矩和稳性力矩所作功之间的动平衡问题。
动稳性:船舶在倾斜过程中计及角因速度和惯性矩的稳性,它研究倾斜力矩可做的力和稳性力短时间所作功之间的动平衡问题。
(2)按倾斜方向
横稳性:指船舶绕纵向轴(X)轴横倾时的稳性
纵稳性:指舰艇绕横向轴(Y)轴纵倾时的稳性
(3)按倾斜角度
所有纵稳性问题都属于小倾角范畴,因为纵稳性力矩大于横稳性力矩,所以不可能因纵稳性不足而导致倾覆。
研究稳性的目的是要求船舶在倾斜后能够产生稳性力矩,该力矩的值应能足以抵御风浪等倾斜力矩迫使船舶倾覆的威胁。
摇荡性,由于过大的稳性将导致居烈的摇摆,对人员,货物,船体 和航海仪器都不利,因此船舶应具有适当的横稳性
二、物体的平衡状态
不倒翁 皮球 铅笔
1、稳定平衡状态
不倒翁的重心很低、当它倾斜时,不倒翁的重力与桌面反作用组成力渴。使不倒翁恢复到原来的站立位置,说明不倒翁具有良好的稳性。
2、中性平衡
皮球是一个球体,重心经于其中心由于桌面反作用力总是通过皮球重心周围。皮球在受外力滚动后,滚到哪里就停在哪里。即皮球不能恢复到原来的位置。
3、不稳定平衡状态
铅笔的重心经过较高至的重力与桌面的反作用力组成力偶,使 铅笔继续倾余,直到倾倒,说明铅笔的稳性不好。
三、浮体的平衡状态
浮体的平衡状态与浮体的重心G,稳心M的相对位置有关。


(1)重心G在稳心M之下,复原力矩![]() 的方向与横倾方向相反,当外力消失后,它能使船舶回复到原来的平衡状态,所以为稳定平衡。
的方向与横倾方向相反,当外力消失后,它能使船舶回复到原来的平衡状态,所以为稳定平衡。![]() 和
和![]() 都为正值。
都为正值。
(2)重心G在稳心M之上,复原力矩的方向与横倾方向相同,它使船舶继续倾斜,所以为不稳定平衡。![]() 和
和![]() 都为负值。
都为负值。
(3)重心G和稳心M重合,![]()
![]() ,当外力消失后,船舶不会回复到原来位置,也不会继续倾斜,成为中性平衡或随遇平衡。
,当外力消失后,船舶不会回复到原来位置,也不会继续倾斜,成为中性平衡或随遇平衡。
(2)、(3)两种情况在造船中是不允许出现的,因为这种船舶在倾斜后不能回复到原来的平衡位置,也就是说,这种船舶的稳性得不到保证。
四、潜体的平衡状态
没入水中的浮体在倾斜某一角度后,其重量W和重心G的位置没有变化,排水体积的形状及浮心的位置也没有变化。因此,它的稳性能完全取决于浮心B和重心G的相对位置。
(1)重心G在浮心B之下,复原力矩![]() 的方向与横倾方向相反,可使浮体回复到原来的平衡状态,称为稳定平衡状态。
的方向与横倾方向相反,可使浮体回复到原来的平衡状态,称为稳定平衡状态。
(2)重心和浮心重合,![]() ,浮体可平衡于任意位置,称为中性平衡或随遇平衡状态。
,浮体可平衡于任意位置,称为中性平衡或随遇平衡状态。
(3)重心G在浮心B之上,复原力矩![]() 的方向与横倾方向相同,因而使浮体继续倾斜而不再回复到原来的平衡位置,称为不稳定平衡状态。
的方向与横倾方向相同,因而使浮体继续倾斜而不再回复到原来的平衡位置,称为不稳定平衡状态。
所以,潜艇在水下状态,重心G必须在浮心B之下,才能得到稳性的保证。
五、初稳性公式
在等体积倾斜条件下,倾斜前后两浮力作用线交于定点M。
![]()
![]()
![]()
初稳性公式的用途:(1)判别水面船舶能否稳定平衡,其衡准条件![]()
![]()
(2)船舶在营动过程中,应用初稳性方程式,处理船内重物移动及装卸重物后,引用船舶的浮态,确定新的![]() 值。
值。
局限性:(1)对于水面船舶当它满足稳定平衡条件时,仅能证明船舶在倾斜力矩消失后,具有能自微倾状态恢复到初始平衡位置的能力而并不说明船舶同时满足不致倾覆的条件。
(2)![]() 其前提为初稳心M是定点,实际上在小倾角范围内是交在定点M(初稳心)附近,因为非常靠近,可以在处理问题时作为交在定点,而用
其前提为初稳心M是定点,实际上在小倾角范围内是交在定点M(初稳心)附近,因为非常靠近,可以在处理问题时作为交在定点,而用![]() 来表示稳性力臂
来表示稳性力臂![]() 这样处理有一定的误差,但
这样处理有一定的误差,但![]() 误差极小。
误差极小。
当倾斜角增大时,误差很明显,![]() 与实际情况不符,当
与实际情况不符,当![]() 增大时,产生两浮力作用线不交于定点M的原因,是由水线上下两部分船体形状决定的,当倾斜水线超出上甲板边缘或舭部(船侧与船底间的弯曲部分称舭部)后,上述误差就变得大。
增大时,产生两浮力作用线不交于定点M的原因,是由水线上下两部分船体形状决定的,当倾斜水线超出上甲板边缘或舭部(船侧与船底间的弯曲部分称舭部)后,上述误差就变得大。
当横倾角度![]() 比较小时
比较小时 ![]()
![]() 取决于排水量,重心高度和浮心移动的距离(?)
取决于排水量,重心高度和浮心移动的距离(?)
船舶在一定排水量下产生微小横倾时,横稳性高![]() 越大,复原力矩
越大,复原力矩![]() 越大,也就是抵抗倾斜力矩的能力越强。因此
越大,也就是抵抗倾斜力矩的能力越强。因此![]() 是衡量初稳性的主要指标。
是衡量初稳性的主要指标。![]() 过大,船舶摇摆周期短,在海上遇到风浪会产生急剧的摇摆;
过大,船舶摇摆周期短,在海上遇到风浪会产生急剧的摇摆;![]() 过小,虽抵抗倾斜力矩的能力较差,但摇摆周期长,摇摆缓和。所以横稳性高是衡量船舶横摇快慢的一个重要特征数。船舶的横稳性高数值与船舶的用途,航区等的不同应在某一合适的范围内(表3-1,表3-2)。
过小,虽抵抗倾斜力矩的能力较差,但摇摆周期长,摇摆缓和。所以横稳性高是衡量船舶横摇快慢的一个重要特征数。船舶的横稳性高数值与船舶的用途,航区等的不同应在某一合适的范围内(表3-1,表3-2)。
![]() 当
当![]() 得到引起船舶横倾
得到引起船舶横倾![]() 的倾斜力矩M。因为倾斜力矩=复原力矩。所以,
的倾斜力矩M。因为倾斜力矩=复原力矩。所以,
![]()
当有横倾力矩![]() 作用在船上。则由此引起的横倾角度为:
作用在船上。则由此引起的横倾角度为:![]() 。
。
同理:纵倾浮态下![]() ————纵稳性公式
————纵稳性公式


纵稳心![]() 与船长L为同一量级较重心高得多。所以在船舶设计中,除浮吊等特种船舶外,一般不考虑纵向稳性问题,在实用上,纵稳性主要是用于求纵倾引起的首尾吃水差,或以此求得新水线的位置。
与船长L为同一量级较重心高得多。所以在船舶设计中,除浮吊等特种船舶外,一般不考虑纵向稳性问题,在实用上,纵稳性主要是用于求纵倾引起的首尾吃水差,或以此求得新水线的位置。
若船长为L,首尾吃水差为t(首倾是取正,尾倾时取负),则纵倾角
![]()
代入纵稳性公式可得:![]()
变形,令![]() 可以求出船舶纵倾1cm所需的纵倾力矩公式为:
可以求出船舶纵倾1cm所需的纵倾力矩公式为:
![]() 每厘米纵倾力矩
每厘米纵倾力矩
由于浮心和重心之间的距离![]() 与纵稳心半径
与纵稳心半径![]() 相比为小值,故可认为
相比为小值,故可认为![]()
![]()
相类似,如有纵倾力矩![]() 作用于船上,由此引起纵倾值
作用于船上,由此引起纵倾值 ![]() (cm)
(cm)
例题P79 例1。
讨论船舶的初稳性,重点是弄清楚浮心B、重心G和稳心M的位置以及三者之间的关系。
六、初稳性高
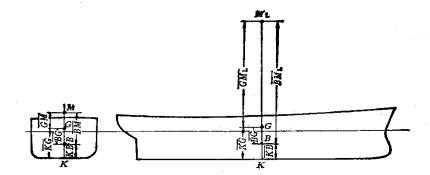

初稳性高![]() 是衡量船舶初稳性的重要指标,可写成
是衡量船舶初稳性的重要指标,可写成
![]()
![]()
![]() 重心高度C或以重心垂向生标
重心高度C或以重心垂向生标![]() 表示。
表示。
浮心垂向坐标 初稳心半径(横稳心半径)
![]()
一般船舶在设计吃水时的初稳性高约等于船宽的4%-6%。
同理:
![]()
纵稳性高的值通常是很大的,一般约等于船长或更大些。
§3-4船舶静水力曲线图
前面讨论了正浮状态下,浮性和初稳性的基本原理及计算,这些计算结果绘制成综合的曲线图即船舶静水力曲线图。分别有下列曲线:P80。15个曲线 1-8浮性曲线(型排水体积曲线、总排水体积曲线、总排水量区县、浮心纵向坐标曲线、浮心垂向坐标曲线、水线面面积曲线、漂心纵向坐标曲线、每厘米吃水吨数TPC曲线) ;9-11稳性曲线(横稳心半径曲线、纵稳心半径曲线、每厘米纵倾力矩MTC曲线) 12-15船型系数曲线(水线面系数![]() 曲线、中横剖面系数
曲线、中横剖面系数![]() 曲线、方形系数
曲线、方形系数![]() 曲线、棱形系数
曲线、棱形系数![]() 曲线)。
曲线)。
静水力曲线计算都是按表格进行的。
§3-5重量移动对船舶浮态及初稳性的影响
在船舶营运过程中装载情况是经常变化的,例如:客货装载情况的不同,航行中燃料、粮食、淡水等消耗物品的变化,重量移动等,所有这些都会引起船的浮态及稳性的变化。
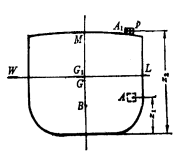 当船上的重量移动时,船的排水量虽然保持不变,但其浮态和初稳性是变化的。为简便计,分别讨论在垂向、横向、纵向的移动情况,再研究在任意方向的移动情况。
当船上的重量移动时,船的排水量虽然保持不变,但其浮态和初稳性是变化的。为简便计,分别讨论在垂向、横向、纵向的移动情况,再研究在任意方向的移动情况。
一、重量的垂向移动
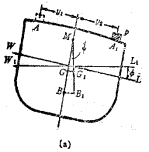
重量![]() 从A点(垂向坐标z1)沿垂直方向移动到A1点(垂向坐标z2)。由于船的排水量和浸水部分的形状都没有发生变化,所以浮心B稳心M的位置保持不变,而船的重心则由原来的G点垂向移动至G1点,根据重心移动原理可知:
从A点(垂向坐标z1)沿垂直方向移动到A1点(垂向坐标z2)。由于船的排水量和浸水部分的形状都没有发生变化,所以浮心B稳心M的位置保持不变,而船的重心则由原来的G点垂向移动至G1点,根据重心移动原理可知:![]()
由于重心的移动引起了初稳性高的改变。新的初稳性高为:
![]() 即
即 ![]()
同理,新的纵稳性高![]() ,数值很大,
,数值很大,![]() 相对于
相对于![]() 来说是小量,实用上常可认为
来说是小量,实用上常可认为![]()
结论:重量垂直向上移动,提高船的重心,初稳性高减小,对稳性不利。
重量垂直向下移动,降低船的垂心,初稳性高增加,对稳性有利。
所以,降低船的重心是提高船舶稳性的有效措施之一。
 二、重量的横向移动
二、重量的横向移动
重量P物体从A点(横向坐标y1)沿横向水平方向移至A1点(横向坐标y2),移动的距离为![]() ,船的重心从原来的G点横向移动到G1点,根据重心移动的原理可得:
,船的重心从原来的G点横向移动到G1点,根据重心移动的原理可得:
![]()
重力的作用线不再与原浮心在同一铅垂线上,因此发生横倾,浮心也自B点向横倾一侧移动。当倾斜到某一角度![]() 时,新的浮心与重心在同一铅垂线上,船就保持新的平衡状态,并浮于新的水线W1L1。
时,新的浮心与重心在同一铅垂线上,船就保持新的平衡状态,并浮于新的水线W1L1。
![]()
用力学的力线平移原理,可求得同样的结果。如果还受到其他外力矩时,此种方种是很有效的。
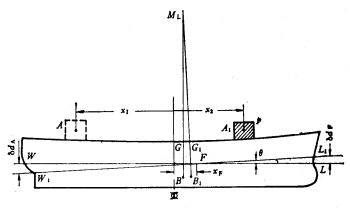 结论:重量的横向移动,使船舶产生了一个横倾角
结论:重量的横向移动,使船舶产生了一个横倾角![]() ,从而减少了甲板进水角的裕度,对船舶稳性是不利的。
,从而减少了甲板进水角的裕度,对船舶稳性是不利的。
三、重量的纵向移动
将船上重量P的货物由A点(纵向坐标x1)沿纵向水平移至A1点(综向坐标x2),移动的距离为![]() 。船的重心由G点移至G1点,因此船发生纵倾,并浮于新的水线W1L1,其纵倾角为
。船的重心由G点移至G1点,因此船发生纵倾,并浮于新的水线W1L1,其纵倾角为![]() ,重量纵向移动后,船的纵倾角为:
,重量纵向移动后,船的纵倾角为:
![]()
纵倾通常用首尾吃水差来表示。§3-2中已证明,等体积倾斜的水线面W1L1 与原水线面WL的交线必然通过WL的漂心F。则有:
![]()
![]()
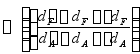
四、任意方向移动
重量P自A点(坐标x1、y1、z1)移至A2点(坐标x2、y2、z2),可以认为:重量沿任意方向移动,由下列三个方向的分位移所组成,即
沿垂直方向的移动![]()
沿水平横向的移动![]()
沿水平纵向的移动![]()
至于船的浮态及稳性所发生的变化,同样可以认为是由三个方向分位移的变化所产生的总结果。即可按照下列步骤求得重量沿任意方向移动后船的浮态及稳性。首先考虑重量沿垂向方向移动,求出新的稳性高![]() 及
及![]() ,再利用已求得的新的稳性高,找出横倾角
,再利用已求得的新的稳性高,找出横倾角![]() 、纵倾角
、纵倾角![]() 及首尾吃水
及首尾吃水![]() 。
。
(1)新的初稳性高(垂向移动)
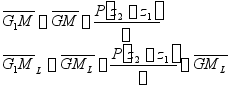
(2)横倾角由下式求得:(横向移动)
![]()
(3)纵倾角由下式求得:(纵向移动)
![]()
(4)首尾吃水的变化:(纵向移动)
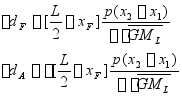
(5)最后船的首尾吃水:(纵向移动)
![]()
必须指出:在讨论上述问题时,是按坐标系统来进行分析的,在应用有关公式计算船的浮态和稳性时,应该弄清正负号的关系,以免发生错误。这里在着重说明一下:x值在船中前为正,在船中后为负;y值在右舷取作正,在左舷取作负;z值在基线以上取作正;横倾角![]() 向右舷倾斜取作正,向左舷倾斜取作负;纵倾角
向右舷倾斜取作正,向左舷倾斜取作负;纵倾角![]() 首倾时取作正,尾倾时取作负。
首倾时取作正,尾倾时取作负。
举例3讨论。
§3—6装卸载荷对船舶浮态及初稳性的影响
重量移动是从某一位置到另一经置,船舶的重量未发生变化,排水量也未发生变化;
而装卸载荷会引起船舶排水量及重心发生变化,从而使船舶的浮态及初稳性发生变化。
现按装卸数量的大小,讨论:小量载荷(<排小量10%)、大量载荷(>排小量10%)
一、装卸小量载荷对船舶浮态及初稳性的影响
在船舶任意位置处增加小量载荷,会使船的吃水增加,并产生横倾和纵倾。为简便起见,分两个步骤讨论:
①假定载荷装载的经置位置在水线面漂心F的垂直线上。只改变船的平均吃水和稳性高,而不产生横倾和纵倾;
②再把载荷移动到指定位置,此时船就产生横倾和纵倾。
1、在漂心垂直线上任意位置装卸载荷对船舶浮态及稳性的影响
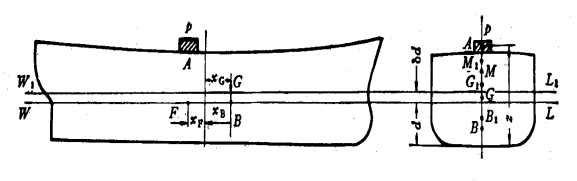

设船原来平浮于水线WL,吃水为d,排水量为![]() ,浮心B、重心G、稳心M、漂心F的位置如图。现将重量为p的载荷装在通过漂心F垂直线上的A处,其坐标为
,浮心B、重心G、稳心M、漂心F的位置如图。现将重量为p的载荷装在通过漂心F垂直线上的A处,其坐标为![]() 。
。
船在增加载荷前平浮于水线WL,这时有:
![]() 和
和 ![]()
增加载荷p后船浮于水线W1L1,平均吃水增量为![]() ,WL与W1L1之间增加的薄层排水体积为
,WL与W1L1之间增加的薄层排水体积为![]() ,则有:
,则有:
![]() ∴
∴ ![]()
表明:载荷p由浮力的增加量![]() 平衡。
平衡。
∵![]() 为小量 ∴WL与
为小量 ∴WL与![]() 非常接近,近似认为
非常接近,近似认为![]() 的体积形心与WL的漂心在同一垂直线上,载荷P与浮力增量
的体积形心与WL的漂心在同一垂直线上,载荷P与浮力增量![]() 的作用点在同一铅垂线上。此时船不产生横倾和纵倾而只是增加平均吃水,其数值为:
的作用点在同一铅垂线上。此时船不产生横倾和纵倾而只是增加平均吃水,其数值为: ![]()
![]() →WL水线面的面积
→WL水线面的面积
而船舶的浮心、重心、稳心由B,G,M→![]()
![]()
![]() ,因而稳性高也由
,因而稳性高也由![]() →
→![]() (?)
(?)![]() 推导。
推导。
先讨论船在横倾某一角度![]() 时复原力矩的情况,设新的初稳性高为
时复原力矩的情况,设新的初稳性高为![]() ,则复原力矩为:
,则复原力矩为:
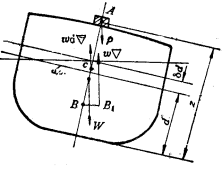
![]() ①
①
复原力矩也可从右图中分析求得:
![]()
![]() 为浮力增量
为浮力增量![]() 的作用点至载荷P的作用点之间的垂向距离,即
的作用点至载荷P的作用点之间的垂向距离,即![]()
![]()
![]()
故 ![]() ②
②
令①=②,比较可得:
![]()
![]()
![]()
增加载菏P的重心高度
根据上式可判断增加载菏P的高度Z对初稳性的影响。
若Z=![]() ,则
,则![]()
若![]() 则
则![]()
若Z![]() 则
则![]()
我们假想在船上有一个平面,高度为![]() ,(称为极限平面或中和平面),当载荷P的重心处于此平面时,对初稳性高无影响。此时排水量将增加,初稳性高不变,而复原力矩会发生变化,为
,(称为极限平面或中和平面),当载荷P的重心处于此平面时,对初稳性高无影响。此时排水量将增加,初稳性高不变,而复原力矩会发生变化,为![]() 。
。
载荷P的重心高于此平面时,初稳性高减小;载荷P的重心低于此平面时,初稳性高增加。
由![]() 可见,
可见,
当![]() ,复原力矩不变; 当
,复原力矩不变; 当![]() ,复原力矩减小
,复原力矩减小
当![]() ,复原力矩增加。
,复原力矩增加。
∴ 若![]() 时,初稳性高减小,复原力矩增加。
时,初稳性高减小,复原力矩增加。
至于增加载荷p对纵稳性的影响,与上述情况相似,可得新的纵稳性高为:
![]()
由于![]() 的数值与
的数值与![]() 相比是小量,可以忽略不计,所以新的纵稳性高可写成:
相比是小量,可以忽略不计,所以新的纵稳性高可写成:
![]()
对于卸除小量载荷的情况,同样可应用上述公式计算船舶的浮态及稳性的影响,只要将P改为-P即可。
2、在任意位置装卸载菏对船舶浮态及稳性的影响
重量P的载荷装在船上![]() 处。
处。
(1)先假定重量P装在![]() (坐标
(坐标![]() ,O,Z)处,则有
,O,Z)处,则有
平均吃水增量 ![]()
新的初稳性高 ![]()
新的纵稳性高 ![]()
(2)将重量P自![]() (
(![]() ,O,Z)移至A(
,O,Z)移至A(![]() 处,则有
处,则有
横倾角 ![]() 纵倾角
纵倾角![]()
首尾吃水的变化为: ![]()
![]()
(3)最后船的首尾吃水为: ![]()
![]()
在卸除小量载荷的情况下,也可应用上述公式,只需将重量P改为-P。
举例4讨论。
二、装卸大量载荷对船舶浮态及初稳性的影响
船上增加或卸除大量的载荷(超过排水量的10%)时,上面公式对船舶浮态和稳性的影响就不够准确了。由于船舶吃水变化较大,新水线与原水线的面积、漂心位置等差别较大。
此时,需要根据静水力曲线图中的有关资料进行计算,所需的静水力曲线资料有:
![]() 排水量
排水量![]() 曲线
曲线
浮心坐标![]() 及
及![]() (即
(即![]() )曲线
)曲线
漂心纵向坐标![]() 曲线
曲线
每厘米纵倾力矩MTC
横稳心半径![]() 曲线
曲线
设船舶原排水量为![]() ,重心坐标:(纵向坐标
,重心坐标:(纵向坐标![]() ,垂向坐标
,垂向坐标![]() ),当船上增加大量载菏P吨(重心坐标为(
),当船上增加大量载菏P吨(重心坐标为(![]() ))后,排水量变为
))后,排水量变为
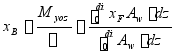
![]()
重心位置 ![]()
![]() (合力矩定理)
(合力矩定理)
![]()

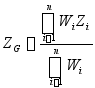
在静水力曲线图横坐标上截取排水量![]() ,从这点作垂线与排水量曲线相交,再从交点引水平线与纵坐标轴相交,得到相应状态下的正浮吃水
,从这点作垂线与排水量曲线相交,再从交点引水平线与纵坐标轴相交,得到相应状态下的正浮吃水![]() 。根据吃水
。根据吃水![]() 从有关曲线上量得
从有关曲线上量得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等值。
等值。
![]() 排水量为
排水量为![]() 时的初稳性高
时的初稳性高 ![]()
![]()
重心![]() 和浮心
和浮心![]() 不一定在同一铅垂线上,即
不一定在同一铅垂线上,即![]() 不一定等于
不一定等于![]() ,则纵倾力矩可求得为:
,则纵倾力矩可求得为:
![]()
船的纵倾值为: ![]()
船的首尾吃水: ![]()
![]()
对于卸除载荷的情况,可用同样的方法计算,不过这时在静水力曲线图的横坐标上应截取的排水量为![]() 和
和![]() ,相应计算中把P改为-P。
,相应计算中把P改为-P。
§3-7自由液面对船舶初稳性的影响
一、自由液面和横倾力矩
1.自由液面
船上通常设燃油舱、淡水舱、压载水舱等舱柜,如果舱内液体(燃油、淡水)未装满,则船舶倾斜时,舱内的液体也将流向倾斜一舷,且液面与水面保持平行,这种自由流动的液面称自由液面。
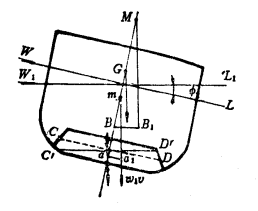 液体流动后,液体体积的形状发生变化,重心向倾斜一侧移动,产生一个倾斜的力矩,此力矩致使舷的稳性降低。
液体流动后,液体体积的形状发生变化,重心向倾斜一侧移动,产生一个倾斜的力矩,此力矩致使舷的稳性降低。
2.横倾力矩
如右图所示,设船的排水量为![]() ,自由液体的体积为v,液体的重量密度为
,自由液体的体积为v,液体的重量密度为![]() ,当船处于正浮状态时,其重心在G点,舱内的自由液面CD平行于水线WL,其重心在a点。当船横倾一小角度
,当船处于正浮状态时,其重心在G点,舱内的自由液面CD平行于水线WL,其重心在a点。当船横倾一小角度![]() 后,舱内液体的自由液面也发生倾斜而变为
后,舱内液体的自由液面也发生倾斜而变为![]() ,且平行于新水线
,且平行于新水线![]() ,其重心由
,其重心由![]() 点移至
点移至![]() 点。设在
点。设在![]() 点加一对大小相等、方向相反的共线力
点加一对大小相等、方向相反的共线力![]() ,则可以看作船的重心不变,但增加了一个横倾力矩,其数值为:
,则可以看作船的重心不变,但增加了一个横倾力矩,其数值为:
![]()
式中:m为自由液体倾斜后重力的作用线和正浮时重力作用线的交点;![]() 为液体重心a至m点的距离。运用§3-2所介绍的船舶等体积倾斜时浮心移动情况,在小倾角范围内,
为液体重心a至m点的距离。运用§3-2所介绍的船舶等体积倾斜时浮心移动情况,在小倾角范围内,![]() 可看作圆弧,m为其圆心,
可看作圆弧,m为其圆心,![]() 为其半径。有横稳心半径
为其半径。有横稳心半径![]() 可得:
可得:
![]()
这样,自由液面产生的横倾力矩可写为:![]()
所以船横倾![]() 角后,除了船舶本身的复原力矩
角后,除了船舶本身的复原力矩![]() 外,还有一个自由液面所产生的倾斜力矩。在这种情况下,船的实际复原力矩为:
外,还有一个自由液面所产生的倾斜力矩。在这种情况下,船的实际复原力矩为:
![]()
 则船的实际初稳性高:
则船的实际初稳性高:![]() 称为自由液面对初稳性高的修正值。其数值只与自由液面的大小、船的排水量有关,而与自由液面的液体体积无关。由上式可见,自由液面的影响使初稳性高减小了
称为自由液面对初稳性高的修正值。其数值只与自由液面的大小、船的排水量有关,而与自由液面的液体体积无关。由上式可见,自由液面的影响使初稳性高减小了![]() 。参照
。参照![]() 式,这个影响相当于把液体的重心由a点提高到了m点,因此m点亦称为自由液面的虚重心。
式,这个影响相当于把液体的重心由a点提高到了m点,因此m点亦称为自由液面的虚重心。
如果船上有几个自由液面的舱柜,则可算出各自的![]() ,然后把它们加起来除以船的排水量,即得所有自由液面对初稳性高的修正值
,然后把它们加起来除以船的排水量,即得所有自由液面对初稳性高的修正值![]() ,此时
,此时
![]()
二、纵稳性
同理,自由液面对纵稳性的影响:
![]()
![]() ——自由液面的面积对其倾斜轴线的惯性矩。
——自由液面的面积对其倾斜轴线的惯性矩。
三、改善初稳性
由![]() 可以看出,自由液面的影响是减小船的初稳性高,也就是降低了船的初稳性。自由液面面积越大,
可以看出,自由液面的影响是减小船的初稳性高,也就是降低了船的初稳性。自由液面面积越大,![]() 也很大,可能使船失掉初稳性。为了减小自由液面对初稳性的不利影响,最有效的办法是使自由液面的面积惯性矩
也很大,可能使船失掉初稳性。为了减小自由液面对初稳性的不利影响,最有效的办法是使自由液面的面积惯性矩![]() 尽量减小,所以可在船内设置纵向舱壁。说明一个设置纵向舱壁对减小自由液面影响的效果。
尽量减小,所以可在船内设置纵向舱壁。说明一个设置纵向舱壁对减小自由液面影响的效果。
设有一个长为l,宽为b的矩形自由液面。在横倾时,该自由液面对于其倾斜轴的惯性矩为:
![]()
若采用纵向舱壁将其分为两个相同的部分,则自由液面![]() 及
及![]() 对于其倾斜轴的面积惯性矩的总和为:
对于其倾斜轴的面积惯性矩的总和为:
![]()
由此可见,用纵向舱壁将自由液面等分后,自由液面对稳性的不利影响可减小至![]() 。同理可以证明,如果用两道纵舱壁将自由液面分成三等分,则其影响可减小至
。同理可以证明,如果用两道纵舱壁将自由液面分成三等分,则其影响可减小至![]() 。进一步推论可得,将舱室进行n等分后,自由液面的影响可减小至未分舱前的
。进一步推论可得,将舱室进行n等分后,自由液面的影响可减小至未分舱前的![]() 。所以,船上宽度较大的油舱、水舱等通常都要设置纵向舱壁。
。所以,船上宽度较大的油舱、水舱等通常都要设置纵向舱壁。
§3—8 悬挂重量对船舶初稳性的影响
船舶的悬挂重量包括:悬挂肉类、救生艇、货物用吊杆装卸、渔船用吊杆起网,以及未固定的悬挂重量等,在船舶倾斜时它们对船舶初稳性会产生不利影响。
 设船上有一未加固定的悬挂于A点的重物p,其重心位于D点,悬线长l,如右图所示。当船横倾一小角度
设船上有一未加固定的悬挂于A点的重物p,其重心位于D点,悬线长l,如右图所示。当船横倾一小角度![]() 后,重物p自D点移至
后,重物p自D点移至![]() 点。若在D点加一对大小相等、方向相反的共线力p,则可看作船的重心不变,但增加了一个横倾力矩,即
点。若在D点加一对大小相等、方向相反的共线力p,则可看作船的重心不变,但增加了一个横倾力矩,即
![]()
则船在横倾![]() 时的实际复原力矩:
时的实际复原力矩:
![]()
则船的实际稳性高:![]()
由上式可见,悬挂重量的影响使初稳性高减小了![]() 。参照
。参照![]() 式,这个影响相当于把重量p自D点垂向移至悬挂点A,故称A点为悬挂重量的虚重心。
式,这个影响相当于把重量p自D点垂向移至悬挂点A,故称A点为悬挂重量的虚重心。
同理,可以求得悬挂重量情况下船的纵稳性高
![]()
最后,介绍装卸液体载荷和悬挂重量对船舶浮态和稳性的影响,计算时必须考虑下列两种影响:
首先,当装卸液体载荷或悬挂重量时,根据装卸载荷公式算出装卸载荷后的稳性高;
![]() 和
和 ![]()
然后再考虑自由液面或悬挂重量对稳性高的影响,求出新的稳性高,并据此进行船舶浮态的计算。
自由液面的影响 ![]() 和
和 ![]()
悬挂重量的影响 ![]() 和
和 ![]()
§3—11 船舶倾斜试验
初稳性高是衡量初稳性的重要指标。
![]()
重心垂向坐标
![]() 横稳性半径
横稳性半径
浮心垂向坐标 根据型线图及型值表精确求出
 船舶设计阶段计算所得的重量和重心位置,与船舶建成后的实际重量和重心位置,有一定差异。故船舶建成以后要进行倾斜试验,以便准确地求得重量及重心的位置,以此作为船舶重量、重心的最终数据。所以,倾斜试验的目的是确定船舶的重量和重心位置,试验的结果要求精确可靠。
船舶设计阶段计算所得的重量和重心位置,与船舶建成后的实际重量和重心位置,有一定差异。故船舶建成以后要进行倾斜试验,以便准确地求得重量及重心的位置,以此作为船舶重量、重心的最终数据。所以,倾斜试验的目的是确定船舶的重量和重心位置,试验的结果要求精确可靠。
一、倾斜试验的原理
如右图所示,当船正浮于水线WL时,其排水量为![]() 。若将船上A处的重物p横向移动某一距离l至
。若将船上A处的重物p横向移动某一距离l至![]() 点,则船将产生横倾并浮于新水线W1L1。此时船的横倾角
点,则船将产生横倾并浮于新水线W1L1。此时船的横倾角![]() 的正切为:
的正切为:
![]()
初稳性高可写为: ![]()
若已知船的排水量![]() 、移动重量p、横向移动距离l,并测量出横倾角
、移动重量p、横向移动距离l,并测量出横倾角![]() ,将它们代入上式后,即得船的初稳性高
,将它们代入上式后,即得船的初稳性高![]() 值。
值。
船的重心垂向坐标即可写成:![]() (
(![]() 、
、![]() 可根据排水量或吃水从静水力曲线图中查得)。
可根据排水量或吃水从静水力曲线图中查得)。
二、试验方法
1、测量首尾吃水和水的重量密度,精确求出排水量。![]()
2、倾斜试验用的移动重物一般是生铁块,将它们分成四组堆放在甲板上指定位置,且![]() ,为形成足够的倾斜力矩使船能产生2°~4°的横倾角(用摆锤进行测量,摆锤用细线挂在船上的o点,下端装有水平标尺;通常船上设2~3个摆锤,分别装在首部、中央、尾部,角度取几个摆锤数值的平均值),移动重物的总重量约为船舶排水量的1~2%,移动的距离l约为船宽的3/4。
,为形成足够的倾斜力矩使船能产生2°~4°的横倾角(用摆锤进行测量,摆锤用细线挂在船上的o点,下端装有水平标尺;通常船上设2~3个摆锤,分别装在首部、中央、尾部,角度取几个摆锤数值的平均值),移动重物的总重量约为船舶排水量的1~2%,移动的距离l约为船宽的3/4。
3、为提高试验结果的精确度,应进行重复倾斜几次,记录并计算每次的横倾力矩M及横倾角![]() ,则可根据
,则可根据![]() 算出各次的
算出各次的![]() 值,然后取其算术平均值,即得船的初稳性高。但在实际计算中,常应用最小二乘法求取
值,然后取其算术平均值,即得船的初稳性高。但在实际计算中,常应用最小二乘法求取

三、试验注意事项
为保证试验的准确性,应注意以下几点:
1、应选风力不大于2级的晴天;
地点:应选在静水的遮蔽处所;
应注意风和水流的影响,尽可能使船首正对风向和水流方向,最好在坞内进行。
2、为了不妨碍船的横倾,应将系泊缆绳全部松开。
3、凡是船上能自行移动的物体都应设法固定,机器停止运转,与试验无关的人员均应离船,留在船上的人员都有固定位置,不能随意走动。
4、船上的各类液体舱柜都应抽空或注满,消除自由液面的影响。如有自由液面则应查明其大小,以便进行修正。
5、试验时,将船上的装载情况以及船上缺少或多余的物资都应进行详细记录,以便将试验结果修正到空载状态。
四、倾斜试验实例
思考题,1。试验的目的确定重量与重心、。
2.题3-16(例5)
第四章 大倾角稳性
§4-1 概述
考虑静力作用,忽略横,纵倾的耦合作用,
![]() 当船在外力矩作用下横倾于某一较大的角度φ
当船在外力矩作用下横倾于某一较大的角度φ
![]() G不变,
G不变,
重力W和浮力△=ω▽形成了一个复原力矩
![]() 复原力臂或静稳性臂
复原力臂或静稳性臂
排水量��������及重心高度KG一定,GZ只随 �������� 而变。
![]()
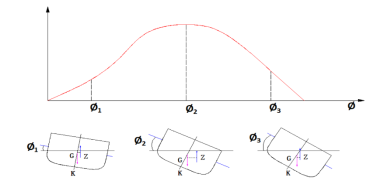
对于小倾角
初稳性假设:
1) 等体积倾斜轴线过正浮水线面的漂心;
2) 浮心移动曲线是一圆弧,圆心为初稳心M,半径为初稳心半径
![]() 大倾角情况下,出水和入水楔形形状不对称,等体积倾斜水线不通过正浮水线面的漂心,浮心的移动曲线在横剖面上的投影不能看作是圆弧,初稳心M不是固定不动,稳心半径 r 随着横倾角φ的不同而变化。此时静稳性臂不能用 表示而应用下式:
大倾角情况下,出水和入水楔形形状不对称,等体积倾斜水线不通过正浮水线面的漂心,浮心的移动曲线在横剖面上的投影不能看作是圆弧,初稳心M不是固定不动,稳心半径 r 随着横倾角φ的不同而变化。此时静稳性臂不能用 表示而应用下式:
![]()
![]() 其中: 为浮心沿水平横向移动的距离,其数值由排水体积的形状决定,称为形状稳性臂。 其数值主要由重心位置决定,称为重量稳性臂 。
其中: 为浮心沿水平横向移动的距离,其数值由排水体积的形状决定,称为形状稳性臂。 其数值主要由重心位置决定,称为重量稳性臂 。
静稳性力臂随��������变化曲线 l=f( �������� )不能用简单的公式表示。根据计算结果绘制的l=f( �������� )图称为静稳性曲线图。它表示船舶在不同倾角时复原力矩(或复原力臂)的大小。
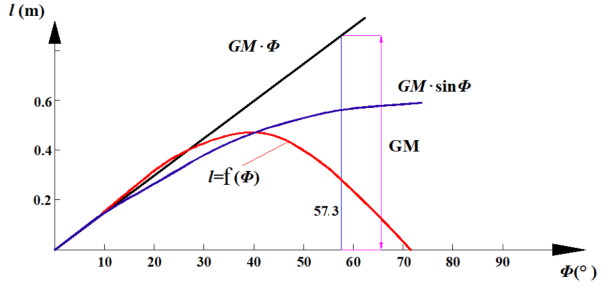
从图中可以看到:在小倾角时,三条曲线基本上是重合的。但是,随着横倾角��������的增加,初稳性公式就不符合实际情况了。
§4-2 船舶静稳性曲线的变排水量计算法
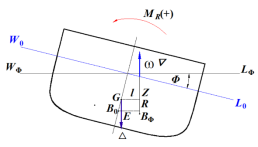 一、基本原理
一、基本原理
交点O 任意确定,船的倾斜为不等体积倾斜
![]()
重量稳性力臂
的大小主要取决于重心的位置。
为使计算问题简便,引入假定重心概念,——规定假定重心不随船舶的装载情况而变,既选定固定的假定重心位置S,计算船舶倾斜后浮力作用线至S点的距离 ls :
![]() 从中我们可以清楚地看到:只要知道横倾后的浮力ω▽作用线的位置,便可立刻得出静稳性臂 。因此,静稳性曲线的计算便可归结为如何求得船舶在横倾后浮力作用线的位置。
从中我们可以清楚地看到:只要知道横倾后的浮力ω▽作用线的位置,便可立刻得出静稳性臂 。因此,静稳性曲线的计算便可归结为如何求得船舶在横倾后浮力作用线的位置。
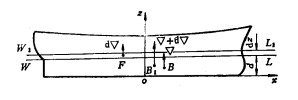
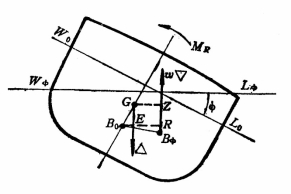
如图所示,船舶正浮于水线W0L0,吃水为d0,排水体积为▽0,浮心在B0处,其高度为KB0。当船舶横倾��������角,假定倾斜水线为W��������L��������,并与W0L0相交于O点。V1为入水楔形的体积,V2为出水楔形的体积,NN为通过O点的计算静矩的参考轴线,c为旋转点O至中心线的距离(即偏离值)。水![]() 线W��������L��������下的排水体积▽�������� 必然是
线W��������L��������下的排水体积▽�������� 必然是
![]()
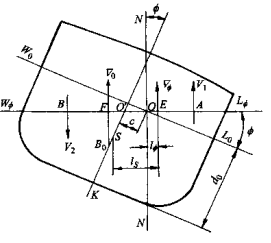
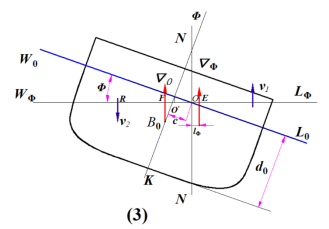
排水体积���������������� 对NN 轴的静矩: (4-4)
船舶浮于倾斜水线 W��������L�������� 时浮力作用线至轴线NN的距离:
![]()
![]()
令
![]()
则(4-4)式为:
![]()
![]() 求l�������� 关键在于:必须首先求得入水楔形和出水楔形体积差:
求l�������� 关键在于:必须首先求得入水楔形和出水楔形体积差:
![]() 以及它们对NN轴线体积静矩:
以及它们对NN轴线体积静矩:
![]() 至于
至于![]() 的数值是容易确定的,
的数值是容易确定的,
从图可看出:
故
 求得lφ后,很容易求出浮力作用线至重力作用线(通过假定重心S)的水平距离:
求得lφ后,很容易求出浮力作用线至重力作用线(通过假定重心S)的水平距离:

有了静稳性臂ls,然后再根据船舶实际装载情况的重心高度KG进行修正,求得静稳性臂:
![]()
![]()
二、������������������������ 和 �������� �������� ��������计算公式
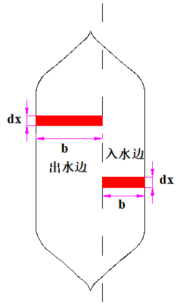
(1)楔形体积差������������������������的计算公式
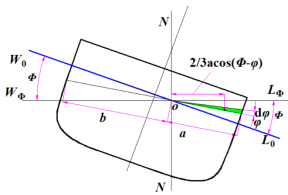
图为船舶横倾��������角度后某一横剖面处的入水和出水楔形
在��������处取一夹角为d��������的小三角形,设底边的距离为a,则小三角形面积
![]()
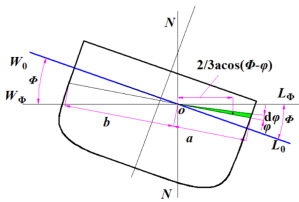
![]() 在船长方向取dx一段,则小三角形的体积为:dAdx,沿整个船长L积分便得到微楔形的体积:
在船长方向取dx一段,则小三角形的体积为:dAdx,沿整个船长L积分便得到微楔形的体积:
在横倾角φ范围内入水楔形体积为
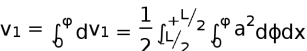
同理求得出水楔形体积:
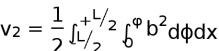
式中:b——出水楔形的水线半宽
入水与出水楔形的体积差:
![]()
(2)楔形体积差静矩Mφ″的计算式
入水小三角形面积对轴NN静矩
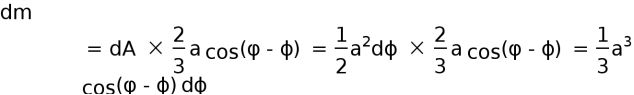
 沿船长积分得微楔形对NN轴的体积静矩
沿船长积分得微楔形对NN轴的体积静矩
![]()
整个入水楔形对NN 轴的体积静矩
![]()
同理出水楔形对NN 轴的体积静矩
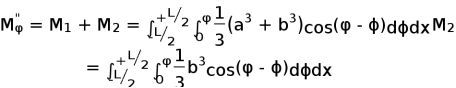
![]() 则 (4-9)
则 (4-9)
水线面W��������L��������对NN 轴线的面积惯性矩 (4-10)
![]()
故式(4-9)也可写作 (4-11)
将式(4-6) 、(4-8) 和(4-11)代入式(4-5),便可得浮力作用线至NN 轴线的距离 l��������:
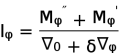
(4-5)
将 l�������� 代入式(4-7),即可求得浮力 ������������������������ 作用线到假定重心的距离ls:
![]()
(4-7)
三、稳性横截曲线
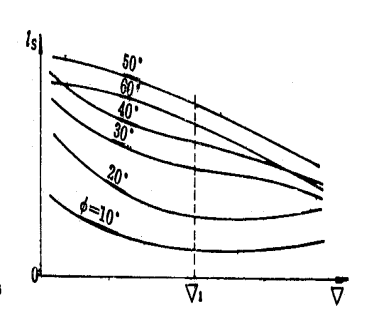
由变排水量法求得不同排水体积����������������在不同横倾角φ 时浮力������������������������作用 线至假定重心S 的距离
l s 。
然后以l s为纵坐标, 以�������� ( ���������������� )为横坐标绘成的曲线称为稳性横截曲线。
再根据稳性横截曲线求出某一排水体积时的ls ,然后对重心加以修正,绘出该装载情况下的静稳性曲线。
以ls为纵坐标,�������� 为横坐标绘制如图所示对应不同横倾角φ的ls =f (�������� )曲线图,该图称为稳性横截曲线图。
稳性横截曲线图
有了稳性横截曲线,可以根据所计算的各种装载情况下的排水量和重心高,按(4-12)式
![]()
计算得到相应船舶各种装载状态情况下的静稳性曲线图。具体可列表进行计算:
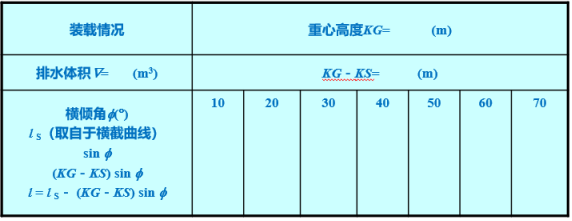
变排水量法的特点:
根据船舶在横倾后的入水和出水楔形所形成的体积矩,求得不同排水体积、不同横倾角时的浮力作用线至假定重心的距离 lS,然后绘制成稳性横截曲线。最后按表4-1 的形式对重心加以修正。
该法不能越过绘制稳性横截曲线图而直接求取某一排水体积下的静稳性曲线。
在所需核算的装载情况较多时或计算船舶改装后的静稳性曲线具有明显的优越性。
四、 具体计算步骤
1. 绘制(9~12个站号)乞氏横剖面图;
2. 选择计算水线、旋转点O、假定重心S位置和横倾角间隔dφ的大小;
3. 量取入水和出水宽度a和b;
4. 计算δ▽φ和Mφ″值;
5. 计算▽φ和 l s 及绘制稳性横截曲线;
6. 绘制静稳性曲线 l=f(φ);
(1) 绘制乞氏剖面
利用AUTOCAD通用软件绘制乞氏剖面,一般取9~12个剖面。乞氏剖面要画到浸水甲板边线并绘出梁拱线。舯前剖面和舯后剖面分别用实线和虚线画出。为了提高计算的准确性,比例应适当取得大些。
(2) 选择计算水线、旋转点、假定重心和横倾角间隔的大小
水线:4-5根,
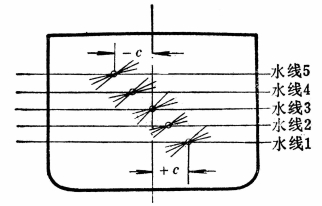 最高:略高于满载水线
最高:略高于满载水线
(旋转点O:偏向出水一舷)
最低:略低于压载水线
(旋转点O:偏向入水一舷)
c:取决于水线至甲板的
距离与吃水之比cc,
cc小:c取大
cc大:c取小
出水为负,入水为正
重心S位置:任意,为方便,一般取在基线上,取 KS=0
横倾角间隔: δφ =10o , φ =70o~80o(海船);
δφ =5o , φ = 35o ~ 40o (江船)
从交点O处量起,凡是到横剖线内侧的入水和出水坐标值 a i和 b i 均取为正值,到横剖线外侧的值都取为负值。
这个规律可以简称为:“内正、外负”
(4) 计算������������������������ 和![]()
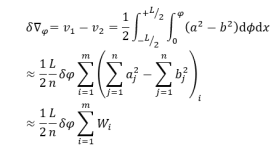 将������������������������和
将������������������������和![]() 的积分公式写成乞氏法则的形式:
的积分公式写成乞氏法则的形式:
![]()
 式中:
式中:
其中:i——为倾斜水线号;j——为乞氏剖面号。
![]()
![]() 以图所示的倾斜水线旋转点为O,按乞氏法表达的 ������������������������ 及 公式分别计算横倾角��������=10o,20o ﹑30o ﹑ 40o 、…时的入水和出水楔形的体积差及其对NN轴线的静矩。
以图所示的倾斜水线旋转点为O,按乞氏法表达的 ������������������������ 及 公式分别计算横倾角��������=10o,20o ﹑30o ﹑ 40o 、…时的入水和出水楔形的体积差及其对NN轴线的静矩。
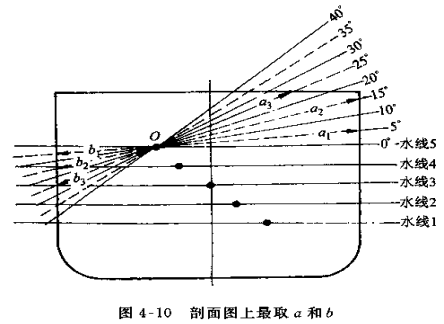
(5) 计算����������������和l ��������及绘制横截曲线
根据计算结果,以l s为纵坐标,以��������为横坐标,绘制各横倾角�������� 的等值线族 l s =f( ��������; �������� = 常数 ),即稳性横截曲线图。
五、计算机程序计算的具体步骤
(1)准备型值表
取各站横剖面型值,按纵向计算法计算。
(2)选择计算倾斜水线、假定重心和横倾间隔大小
计算的倾斜水线一般取5—7根。最高倾斜水线一般与中横剖面的左上角相切,最低倾斜水线一般与中横剖面的右下角相切,各中间水线的位置在最高倾斜木线和最低倾斜水线之间,等间距或不等间距均可。
重心取在基线上,KS=0;倾角间隔海船����������������=10o,��������=80o;江船����������������=5o,��������=50o。
(3)计算复原力臂
分别计算各倾斜水线下的排水体积����������������和浮心B�������� (y��������, z��������), 假定重心高zS为零,计算复原力臂ls
![]()
![]()
(4) 根据����������������和ls绘制稳性横截曲线
(5) 绘制静稳性曲线
§4-3 船舶静稳性曲线的等排水量计算法
一、基本原理
首先确定各倾角的等体积倾斜水线,然后计算各线下的浮心B��������(y�������� , z��������),再按公式 ls=y��������sin��������+z��������cos��������计算假定zS为零的复原力臂ls,最后根据ZG按公式l=ls-zGsin�������� 计算各倾角下的复原力臂l,并绘制排水量��������时的静稳性曲线l=f(��������)。
二、具体计算步骤
首先用迭代法计算各倾角下的等体积倾斜水线,再按基本原理的步骤计算静稳性曲线。
§4-4上层建筑及自由液面对静稳性曲线的影响(自学)
上节中得到的静稳性曲线只计算到船体主体部分(即上甲板)为止。但对于具有水密上层建筑,如满足规范的要求,也可计入上层建筑对静稳性曲线的影响。因为水密的上层建筑在入水后也产生相应的浮力和复原力矩。此外,船内设有一定数量的燃油舱、淡水舱和压载水舱,当它们具有自由液面时,舱内的液体重心将随着船舶倾斜而移动,形成一个倾斜力矩。因此,在船舶主体的静稳性曲线计算完毕后,有时还需计算上层建筑和自由液面对稳性的影响,并进行必要的修正。
§4-5 静稳性曲线的特征
曲线在原点O处的斜率
最大静稳性臂及其对应的横倾角
稳性范围以及曲线下的面积——这些对于判断船舶的稳性非常重要。
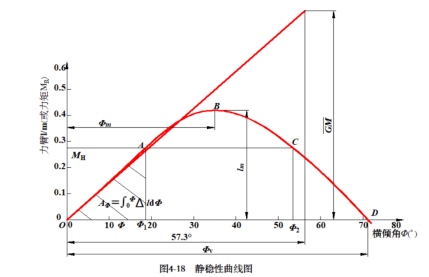
一、 静稳性曲线的特征
(1) 静稳性曲线在原点处的斜率
船舶倾斜一角度φ后的静稳性臂:
![]()
将上式对φ求导得:
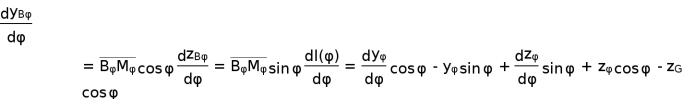
将 代入上式得:
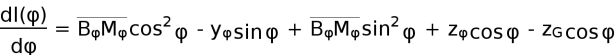
![]()
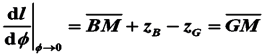
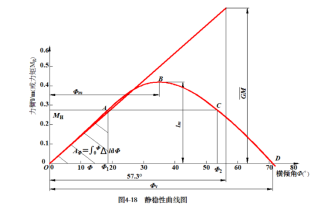 静稳性臂曲线在原点处的斜率等于初稳性高GM。在小角度时,静稳性臂与横倾角成正比,即 l = GM·�������� 。
静稳性臂曲线在原点处的斜率等于初稳性高GM。在小角度时,静稳性臂与横倾角成正比,即 l = GM·�������� 。
(2)最大复原力臂l m及其对应的横倾角φm
静稳性曲线的最高点B的纵坐标值是船舶在横倾过程中所具有的最大复原力矩(或复原力臂),表示船舶所能承受的最大静态横倾力矩。若外来的恒定(静态)横倾力矩超过此值,则船将倾覆。因此,B点的纵坐标值称为最大复原力矩(或力臂l m),其对应的横倾角(B点横坐标值)称为极限静倾角φm。
(3)稳定平衡与不稳定平衡
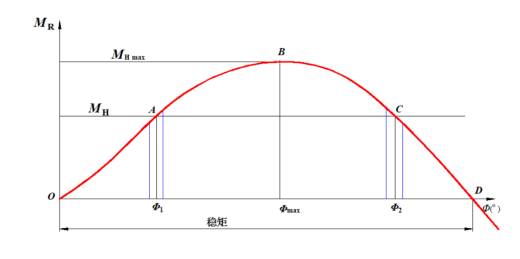
如图所示,当恒定横倾力矩小于最大复原力矩时,代表该横倾力矩的水平线与静稳性曲线相交于A、C两点,其相应的横倾角为��������1和��������2。但此时船舶的静倾角应该是��������1,理由如下:在��������1附近若再有一小扰动,使横倾角略微增大(或减小),则复原力矩大于(或小于)横倾力矩,船将返回到原��������1,因此��������1是处于稳定平衡状态;
但当在��������2附近若有一小扰动,使横倾角略微增大,则复原力矩小于横倾力矩,船将进一步横倾直至倾覆,如果该扰动使横倾角略微减小,则复原力矩大于横倾力矩,船的横倾角将继续减小直至返回到��������1处的平衡位置,因此船在��������2处是处于不稳定平衡状态。
由上述分析可推知:船在恒定横倾力矩作用下一般有两个平衡位置,分别处于静稳性曲线上升线(O-B段)的交点和下降段(B-D段)的交点,在上升段的交点为稳定平衡位置,而在下降段的交点为不稳定平衡位置。
(3) 稳性消失角及稳距
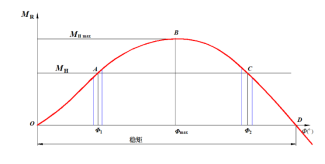
在静稳性曲线上的D点,其复原力矩 MR =0,与之相对应的横倾角��������V为稳性消失角。OD之间的距离称为稳距,表示船舶在该段范围内是具有复原力矩的。当横倾角超过稳性消失角��������V后,船的复原力矩变为负值。其作用使船舶继续倾斜直至倾覆。稳性消失角��������V也是表示船舶稳性好坏的标志之一。
(5)稳性曲线下的面积
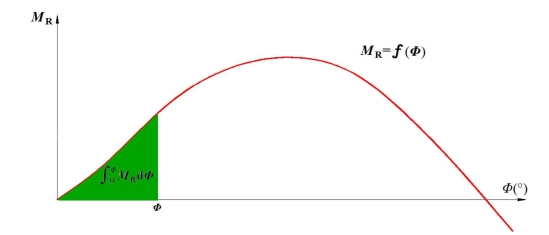
![]() 从力学中知道,力矩乘以转角等于功。船舶在倾斜力矩作用下产生横倾,如果倾斜力矩是静力性质的,那么,倾斜力矩恰好与船舶的复原力矩相平衡,倾斜力矩所作的功全部转化为船舶的位能,即
从力学中知道,力矩乘以转角等于功。船舶在倾斜力矩作用下产生横倾,如果倾斜力矩是静力性质的,那么,倾斜力矩恰好与船舶的复原力矩相平衡,倾斜力矩所作的功全部转化为船舶的位能,即
上式表明,倾斜力矩所作的功,或者说船舶倾斜后所具有的位能等于静稳性曲线下的面积。显然,静稳性曲线下的面积愈大,船舶的稳性愈好。因此,静稳性曲线下的面积也是表征船舶稳性的一个重要标志。
实际上,静稳性曲线的特征值,如原点处的斜率、最大复原力矩和极限静倾角、稳距或消失角等已大致限定了静稳性曲线的轮廓及面积。而且这些特征值都是表征船舶稳性的重要标志,因此《海船法定检验技术规则》中对其数值都有明确的规定。
典型的静稳性曲线图
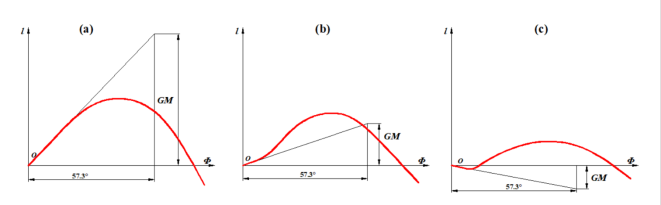
a)—初稳性高较大,静稳性臂的最大值也不小,稳性消失角可达60 0 ~90 0。具有这种静稳性曲线的船舶一般船宽较大、干舷较小,如江船之类。通常这类船舶的稳性是足够的,但遇到风浪时会产生剧烈的摇摆,对于海船来说并不理想。
b)—初稳性高较小,但曲线很快地超出在原点处的切线,静稳性臂的最大值也不小,稳性范围较大。形状较为理想。具有这种静稳性曲线的船舶一般干舷较高,如海船,通常这类船舷的大倾角稳性是足够的,遇到风浪时摇摆相对较缓和,这种静稳性曲线较为理想。
c)—初稳性高为负值,这种船在静水中虽然不会翻掉,但因正浮位置是不稳定平衡,故具有一永倾角,其大倾角稳性较差。一般不允许出现这种情况 。
§4-6 动稳性
一、 基本概念
前面讨论的船舶稳性问题,都是属于静稳性范畴。即假定外力矩逐渐作用在船上,船在倾斜过程中倾斜得很慢,因而认为角速度等于零。
但实际船舶在海上航行时经常受到外力矩MH的突然作用,如阵风的突然吹袭、海浪的猛烈冲击等。船舶受到外力矩MH的突然作用很快地产生倾斜,在倾斜过程中具有一定的角速度,这种情况与静力作用完全不同。
假定外力矩逐渐作用在船上,船在倾斜过程中,外力矩(图中白色线)经常保持等于复原力矩,船倾斜得很慢,因而认为角速度等于零。当外力矩MH不再增加时,船即平衡于某一横倾角 ��������1 ,称为静横倾角。船上横向移动重物或在船的一侧装卸小量货物等情况,都可以看作是外力矩的静力作用。
在复原过程中,船舶的运动情况是:
(1)在倾角��������=��������d 至��������1之间; MR>MH ,船舶加速复原。
(2)当��������=��������1时,MR=MH,复原力矩已不能再使船舶复原,但由于船舶具有角加速度,故将继续复原。
(3)在倾角��������=��������1至0之间, MH>MR ,船的复原速度减小。
(4)在倾角��������=0时,船的复原速度等于零而停止复原。但这时MR= 0 ,外力矩MH又使船产生倾斜。
这样,船舶将在倾角0与��������d之间往复摆动,但由于水及空气阻力的作用,船的摆动角速度逐渐减小,最后将平衡于��������1处。船在动力作用下的最大横倾角��������d 称为 动横倾角。
船舶在外力矩的动力作用下,即使已经达到了MR=MH,船舶仍将继续倾斜,直至��������d时才开始复原运动。显而易见,动横倾角��������d 较静横倾角��������1要大很多,这是比较危险的情况,故在讨论船舶的大倾角稳性时,必须研究动稳性问题。
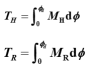 在外力矩的动力作用下,船舶倾斜时具有一定的角速度,只有当外力矩MH所作的功完全由复原力矩MR所做的功抵消时,船的角速度才变为零而停止倾斜。根据这个原理,我们可以决定动力作用下的动横倾角��������d 。
在外力矩的动力作用下,船舶倾斜时具有一定的角速度,只有当外力矩MH所作的功完全由复原力矩MR所做的功抵消时,船的角速度才变为零而停止倾斜。根据这个原理,我们可以决定动力作用下的动横倾角��������d 。
当船舶由��������=0倾斜至��������d时,外力矩MH所做的功
复原力矩MR在��������=0与��������d之间所做的功
从图中可以看出:TH为曲线MH所围面积OEDC,TR为此曲线所围的面积OABC。因此,面积OEDC=面积OABC,表示外力矩所作的功等于复原力矩所做的功,由于面积OADC为两者所共有,故面积OEA=面积ABD(图中阴影线部分),D点所对应的倾斜角即为动横倾角��������d。
![]() 二、动稳性曲线
二、动稳性曲线
当船舶横倾至 �������� 时,复原力矩MR所作的功:
![]() 式中:复原力矩MR 随 �������� 的变化规律是由静稳性曲线来表示的,如图所示。由于复原力矩MR=��������×l,所作的功又可写成:
式中:复原力矩MR 随 �������� 的变化规律是由静稳性曲线来表示的,如图所示。由于复原力矩MR=��������×l,所作的功又可写成:
式中:ld 称为动稳性臂;TR或 ld随 �������� 而变化的曲线称为动稳性曲线。
动稳性曲线是静稳性曲线的积分曲线,有了静稳性曲线(MR或 l ),就可以用近似计算方法求出动稳性曲线( TR 或 ld )。
静稳性的线和动稳性曲线之间有下列关系:
(1)在 ��������= 0处,静稳性臂l和动稳性臂ld都为零,这是 ld的最小值。
(2)当 �������� 等于极限静倾角��������max时,静稳性臂达最大值 l max ,在动稳性臂ld曲线上表现为反曲点A’。
(3)当 �������� 等于稳性消失角时, l=0,动稳性臂 ld达最大值 ld max。
(4)动稳性曲线在某一倾角处的纵坐标代表静稳性曲线至该处所围的面积,例如,在图中,动稳性曲线的纵坐标A’C’代表静稳性曲线图的面积OAC;动稳性曲线的纵坐标B’D’代表静稳性曲线图的面积OAB。
三、静稳性和动稳性曲线的应用
(1)动横倾角的确定
风力F 作用产生横漂,于是,水下部分则受到一个水阻力R 作用。在稳定状态下,两个力大小相等,方向相反。由于不在同一水平线上,因而形成了一个使船横倾的力矩: Mf=F× z f
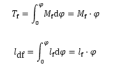 通常直接应用动稳性曲线来求取动横倾角��������d。显然,恒风作用下的横倾力矩Mf 所作的功 T f 和横倾力臂l df分别为:
通常直接应用动稳性曲线来求取动横倾角��������d。显然,恒风作用下的横倾力矩Mf 所作的功 T f 和横倾力臂l df分别为:
是一横直线,其斜率为M f 和 l f。
当取��������=1弧度=57.3°时,有 T f = Mf 或 l d f = lf ,这样,我们可在图的横坐标上量取Mf 或lf 得N点,连接ON ,则直线ON 即为T f 或 ld f 随�������� 而变化的规律。
横倾力矩所作的功T f (或 ld f )与复原力矩所作的功T R (或 ld )曲线的交点 C ’ 表示横倾力矩Mf 所作的功与复原力矩 MR所作的功相等。因此,与 C ’点相对应的倾角即为动横倾角 ��������d 。
(2)阵风作用下船舶所能承受的最大风倾力矩Mfmax
在静稳性曲线图上,作一水平线并使面积OFG = 面积 GHK,K点落在静稳性曲线的下降段上,过此以后不复有两个力矩作功相等的可能,则OF 即为所求的最大风倾力矩Mf max (或力臂
lf max ),K点相对应的倾角称为极限动横倾角��������dmax。
在动稳性曲线图上,过O点作与动稳性曲线相切的切线OK’,此直线表示最大风倾力矩所作的功,直线在 ��������=1 弧度=57.3° 处的纵坐标便是所求的最大风倾力矩,切点K’相对应的倾角便是极限动横倾角��������d max 。
(3)在风浪联合作用下,船舶所能承受的最大倾斜力矩M f max (或力臂l f max )
船舶受到波浪作用产生摇摆,当船向迎风一舷横摇至最大摆幅��������0 并刚往回横摇时,突然受到一阵风的吹袭,此时船最危险。这是因为这时复原力矩的方向与风倾力矩的方向一致,两个力矩加在一起促使船舶倾斜加剧。
由于船舶是左右对称的,故其静、动稳性曲线必对称于O点。在图上截取OG= ��������0 ,作水平线BE,令GB=Mf,并使面积ABC=面积CDE ,与D点对应的即为动横倾角��������d 。
若不考虑横摇角��������0 ,在同样的Mf 作用下,动横倾角��������d’ 要比��������d小得多。同样在动稳性曲线图上,向左量��������0 ,在动稳性曲线上得A’点,由A’沿横轴取57.3°,作垂线,截取B’N’=Mf,连A’N’与动稳性曲线交于D’点, D’相对应的横倾角即为��������d 。由两图所得是完全一致的。
M f max (或l f max )的确定
在静稳性曲线图上,作水平线 FL使面积AFH=面积HKL,L 恰在静稳性曲线下降段上,则GF即为船舶在风浪联合作用下所能承受的最大倾斜力矩M f max (或力臂l f max )。
MH max 是船舶正浮时在静力作用下所能承受的最大倾斜力矩,对应的倾角��������1称为极限静倾角;
Mfmax是船舶正浮时,在阵风作用下所能承受的最大倾斜力矩
M’f max 是船舶在阵风和波浪联合作用下,即考虑共振横摇角0时所能承受的最大倾斜力矩
M H max > M f max > M ’f max ,其对应的横倾角 ��������1< ��������d < ��������d’
从船舶是否会倾覆来说,M ’f max使船倾覆的最小力矩,称作最小倾覆力矩(或力臂),常记作 Mq ( lq ) , ��������d’ 叫极限动倾角,记作 ��������d max,它表示船舶所允许横倾的最大角度。
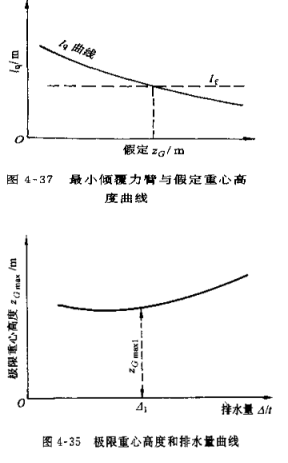
最小倾覆力矩M q(或力臂l q )的确定
在动稳性曲线上过A’点作动稳性曲线的切线A’L’,再从A’沿水平方向取57.3°,作垂线与A’L’交于一点,则该点在过A’点的水平线以上的纵坐标即为Mq (或lq ) ,切点L’对应的角度为��������d max。
从上可见,考虑横摇角��������0的情况,对船舶来说最危险,因此,我们总是依据风浪联合作用的情况来进行大倾角稳性的核算。
这里需说明两点:
(1)外力矩一般是随横倾角��������变化的,特别是风力矩,而且多半是随着��������的增加而减小。像美国就假定风力矩随cos2��������变化,中国和日本的规范则取为不随而变的定值。这样做可使计算、作图简便:外力矩在静稳性曲线图上是一水平线,在动稳性曲线图上是一斜直线,对作图极为方便,而且这样选取在实用上是偏于安全的。但绝不能造成一种错觉:外力矩总是不变的。
(2)用动稳性曲线求解要比用静稳性曲线方便,省去了凑面积相等的步骤。但是动稳性曲线的这一优点,只有当外力矩的积分曲线是一直线时才显示出来(即外力矩为定值)。在国外很多规范中,规定外力矩是变化的,在进行大倾角急性计算时用静稳性曲线反而更方便。
四、进水角和进水角曲线
1. 进水角φE
船舶的甲板及上层建筑的侧壁上有许多开口(例如舱口、门和窗等),如果这些开口不是水密的,则当船舶倾斜时,水面达到某一开口,海水将灌入船身主体内部,使船舶处于危险状态。因此,当倾斜水线到达该开口处即认为船舶丧失稳性。故在稳性校核时,还要计算水线到达最先进水的那个非水密处的倾斜角度φE ,φE即称为进水角。
进水角以后的静稳性曲线不再计及,使稳性的有效范围缩小,从而也就降低了船舶的抗风浪能力。
2.进水角曲线
船舶的进水角φE 随排水体积��������的变化而变化,随排水体积变化的曲线称为进水角曲线。
设 E点为船上最先进水的非水密开口下缘,过E点作与水平线成倾角��������1 ,��������2, …, ��������5的各倾斜水线,算出各倾斜水线下的排水体积��������1 , ��������2 , �������� 3 … 。然后以进水角为纵坐标,排水体积为横坐标绘制曲线 ��������E= f (��������)。
根据排水体积查得进水角,由进水角确定船舶稳性曲线的有效部分,再根据稳性曲线的有效部分,来决定船舶的最小倾覆力矩Mq (或力臂lq )。
§4-7 船舶在各种装载情况下的稳性校核计算
如何根据稳性规范进行船舶的稳性校校。关于船舶稳性的衡准,世界各国都有他们自己的规范。本节只简要地介绍我国船舶检验局在1999年颁布的《船舶与海上设施法定检验规则》简称《海船法规》,而且着重介绍对稳性的基本要求及有关规定和大体核算步骤。根据《船舶与海上设施法定检验规则》的要求,如果船舶在各种装载情况下的稳性都能满足,则认为所设计的船舶具有足够的稳性。
基本假设:《海船法规》是假定船舶没有航速,受横浪作用发生共振横摇,当摇至迎风一舷最大摆幅 ��������0 时,受一阵风作用而不致倾覆,《海船法规》把此海况作为船舶可能遇到的最危险情况来考虑,有关的衡准、规定都是由此前提出发的。
船舶的稳性随装载情况变化,为确保船舶在所有的装载情况都有足够的稳性,需要对几种典型的装载情况进行稳性校核。例如,普通货船需要进行稳性计算的装载情况有;满载出港、满载到港、空载(或加压载)出港和空载(或加压载)到港四种。
除上述四种典型装载情况外,如有对稳性更不利的其他情况也应进行核算,例如航行于冰区的船舶,应考虑船体水线以上部分因结冰而对稳性的影响。此外,船的类型不同,所要核算的装载情况亦不同,《海船法定检验技术规则》对此都有明确的规定。
一、 稳性衡准数
稳性衡准数是对船舶稳性的重要基本要求之一。《海船法规》规定:船舶在所核算的各种装载情况下的稳性,稳性衡准数应 K 符合下列不等式:
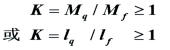
式中:Mq(l q )—最小倾覆力矩(力臂),表示船舶在最危险情况下 抵抗外力矩的极限能力;
Mf(l f )— 风压倾斜力矩(力臂) ,表示在恶劣海况下风对船舶作用的动倾力臂
K ≥1表示了风压倾斜力矩小于使船舶倾覆所必须的最小倾覆力矩(至多是相等),所以船舶不至于倾覆,因而认为具有足够的稳性。
(1)最小倾覆力矩(或力臂)的计算
M q (或 l q )是根据静稳性曲线或动稳性曲线以及横摇角来确定的。计算时使用的稳性曲线必须是经过自由液面修正和考虑了进水角影响后的曲线,若有上层建筑也应考虑在内。
关于��������0 的计算是基于船舶零航速且横对波浪。我们知道,船舶在波浪中航行对,其横摇的程度不仅与波浪有关而且与船型、船舶装载情况、附体等因素有关。
![]() 《海船法规》第七篇完整稳性中规定对有舭龙骨的圆舭形船舶,横摇角��������0按下列公式计算:
《海船法规》第七篇完整稳性中规定对有舭龙骨的圆舭形船舶,横摇角��������0按下列公式计算:
式中:C1 、 C2 、C3 、 C4 —— 系数。
系数C1的选取:
![]() 船舶的自摇周期Tφ等于波浪周期Tw时,横摇最严重,系数C1根据船舶的自摇周期及航区由图查得。
船舶的自摇周期Tφ等于波浪周期Tw时,横摇最严重,系数C1根据船舶的自摇周期及航区由图查得。
式中:GM0——所核算装载情况下船舶未计及自由液面修正的初稳性高(m);
B——不包括船壳板的最大船宽(m);
KG——核算装载情况下船自重心至基线的垂向高度(m);
f——系数,按般舶的B/d值自下表查得。
B/d | 2.5以下 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0以上 |
f | 1.0 | 1.03 | 1.07 | 1.10 | 1.14 | 1.17 | 1.21 | 1.24 | 1.27 | 1.3 |
当 T�������� >20s时 , C1取0.19。
规则把航区分为四类,即远海(远洋)航区、近海航区、沿海航区和遮蔽航区,船舶的稳性按此四类不同航区进行核算。
(1)远洋航区是指无限航区;
(2)近海航区是指渤海、黄海及东海中距岸不超过200海里的海域,台湾海峡,南海中距岸不超过120海里(海南岛东海岸及南海岸距岸不超过50海里) 海域;
(3)沿海航区是指比近海航区距岸更近的海区,一般为10~20海里的海域;
(4)遮蔽航区是指沿海航区内遮蔽条件较好、波浪较小,且岛屿与海岸之间距离不超过10海里(但台湾海峡沿岸海域内,上述距离减半)的海域。
由此可见,航区的划分实际上反映了对风浪大小不同的考虑,航行于不同航区的船舶必然受到不同风浪的作用。
系数C2主要与波浪的有效波倾角有关,主要反映出与重心高和吃水比有关,按下式计算:
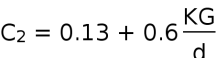
当C2 >1时,取C2 =1.0;当C2 >0.68时,取C2 =0.68。
系数C3主要与船舶的宽度吃水比B/d有关,按下表查得。
B/d | 2.5以下 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0以上 |
C3 | 1.011 | 0.013 | 0.015 | 0.017 | 0.018 | 0.019 | 0.020 | 0.021 | 0.022 | 0.023 |
系数C4主要与船舶的类型和舭龙骨的尺寸有关,按下表查得。
A b/LB(%) | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 及以上 |
干货船 油船 集装箱船 海驳 | 1.000 | 0.754 | 0.685 | 0.654 | 0.615 | 0.577 | 0.523 | 0.523 | 0.523 |
客船 渔船 拖船 | 1.000 | 0.885 | 0.823 | 0.769 | 0.708 | 0.654 | 0.577 | 0.546 | 0.523 |
表中A b是舭龙骨的总面积(m2),L为垂线间长(m),B为型宽(m)。对于有方龙骨的船舶,可将其侧面积计入舭龙骨面积A b之内。对于装有减摇鳍的船舶,计算��������0时,不应计入其作用,但减摇鳍面积可计入舭龙骨面积。 B/d的比值和舭龙骨尺寸愈大,则��������0愈小。
对其他特殊线型的船舶,C2、C3和C4应经验船部门同意后采用。对水线以下尖舭型船舶,![]() 。可按下式计算:
。可按下式计算:![]()
式中 φ0 为相应于无舭龙骨圆舭型船的横摇角。
![]() (2)风压倾斜力矩(或力臂)的计算
(2)风压倾斜力矩(或力臂)的计算
风压倾斜力矩(或力臂)可按下式求得:
式中:A f ——船舶受风面积(m2),即船体水线以上部分的侧投影面积;
z——船舶受风面积中心至水线的距离(m),即计算风力作用力臂;
��������——所核算装载情况下的船舶排水量
p ——单位计算风压(Pa),根据航区和受风面积中心至水线的距离z由表查得。
航区 | 风压作用力臂z(m) | ||||||
1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | |
远海航区 | 829 | 905 | 976 | 1040 | 1099 | 1145 | 1185 |
近海航区 | 448 | 493 | 536 | 574 | 603 | 628 | 647 |
沿海、遮蔽航区 | 228 | 248 | 268 | 284 | 301 | 314 | 326 |
航区 | 风压作用力臂z(m) | ||||||
4.5 | 5.0 | 5.5 | 6.0 | 6.5 | ��������7.0 |
| |
远海航区 | 1219 | 1249 | 1276 | 1302 | 1324 | 1347 |
|
近海航区 | 667 | 683 | 698 | 711 | 724 | 736 |
|
沿海、遮蔽航区 | 336 | 343 | 350 | 357 | 363 | 368 |
|
二、初稳性高和静稳性曲线
我国《海船法规》第4篇 船舶安全第七章 完整稳性中规定:船舶在各种装载情况下经过自由液面修正后的初稳性高和静稳性曲线应满足下列要求:
(1)初稳性高应不小于0.15m。
(2)横倾角�������� =30°处的复原力臂 l 应不小于0.2m。如船体有进水角且进水角��������E<30°,则进水角处的复原力臂 l 应不小于0.2m。
(3)最大复原力臂所对应的横倾��������max应不小于30° 。 当船舶的船宽型深比B/D大于2时,最大复原力臂所对应的横倾角应不小于:![]()
式中:D——船舶型深(m),
B——不包括船壳板的最大船宽(m)。当B>2.5D时,取 2.5D;
K——计算所得的稳性衡准数,当K>1.5时取K=1.5。
对遮蔽航区的船舶,如静稳性曲线特征值不能满足上述的(2) 、(3)等要求时,允许降低要求,但必须满足以下规定:
(1)最大复原力臂对应的横倾角��������max不小于150。
![]() (2)最大复原力臂值 lm应不小于下式规定之值:
(2)最大复原力臂值 lm应不小于下式规定之值:
式中: ��������m——最大复原力臂对应角,(º������)
(3)进水角 ��������E 不小于最大复原力臂值 lm 的对应角��������max
若船舶在营运过程中,其纵倾等于或超过某一定数值或者船舶的形状和布置使船舶产生大的横倾从而造成横倾的变化对��������E和 l 产生可观影响时,这些横倾的变化影响应计入。
上述四项规定也是对船舶稳性的基本要求,这些规定实际上限定了静稳性曲线的面积和形状。
国际航行海船的稳性校核计算可参阅《国际航行海船法定检验技术规则》,其基本原理相同,但具体规定和形式有所不同,与国际海事组织IMO的有关稳性的规则一致。
内河(包括长江)船的稳性计算和校核原理与海船大体相同,但具体公式和标准数据是有区别的,详细情况可参阅《内河船舶法定检验技术规则》。
对于船长在30 m以下的内河小型船舶,一般说来不必进行大倾角稳性计算,有关这类船舶的稳性校核方法,可参阅《长江水系小型钢船建造规范》。
对船舶稳性衔准的基本思想概括说明如下:稳性曲线只表示了船舶本身所具有抵抗外力矩的能力,或者说,只表示了船舶本身所具有的稳性能力,至于船舶受到的力矩究竟有多大,以及是否经受得住,这要看外力矩的作用情况面定。外力矩主要来自风浪的作用,而风浪的大小又与离岸距离及水域开阔程度等因素有关。
因此《海船法定枪验技术规则》中,把航区分为四类:即远海(无限)、近海、沿海和遮蔽航区;对内河,《内河船舶法定检验技术规则》则把航区划分为三级:即A、B、C级航区,另加J级(急流江段),并以此作为计算外力的依据。对于拖船和客船,除风浪作用外,还会受到其他外力作用,这些在规则中都有明确规定,这里不再重复。
§4-8 极限(许用)重心高度曲线
极限(许用)重心高度指在各种装载情况下船舶恰好能满足稳性要求时的重心高度。船舶在实际营运中重心高度不可超过此极限值,否则便会造成稳性不足,航海安全得不到保证。
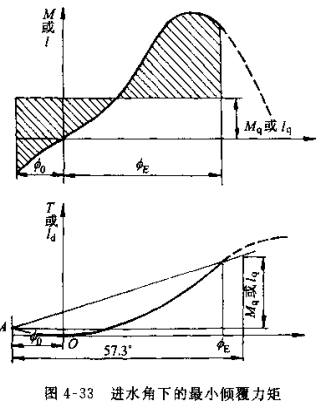
船舶在各种装载情况时(即不同排水量时)都有相应的极限重心高度。将船舶在不同排水量(通常包括该船营运时可能的排水量变化范围)时的极限重心高度连成曲线,则该曲线称为极限重心高度曲线。
对于不同的稳性要求,都有其对应的极限重心高度曲线,实际上采用的极限重心高度曲线应是船舶满足所需规范稳性要求(如满足中国船级社的完整稳性要求、满足中国船级社的破损稳性要求等)的各极限重心高度曲线的下限包络线。

图所示的极限重心高度曲线就是表示这种关系的简便形式。横坐标为排水量�������� (t),纵坐标为极限重心高度zGmax (m)。船舶在排水量��������1时的极限重心高度为zGmax1,若船舶在该排水量时的实际重心高度zG1较zGmax1小,则船舶稳性是足够的。反之,稳性不足。
下面简要介绍船舶在某一排水量时极限重心高度计算方法。以我国《海船法定检验技术规则》对国内航行船舶(普通货船) 完整稳性要求为例,有下列几项要求:
(1)经过自由液面修正后初稳性高度GM不小于0.15m。
(2)横倾角φ=300处的复原力臂l30应不小于0.2m。
如船体进水角φE<300, 则进水角处的复原力臂应不小于该规定值。
(3)船舶最大复原力臂所对应的横倾角(极限静倾角)
φm应不小于300。
(4)稳性衡准数K应不小于1。
因此,对于以上各项要求都有其相应的极限重心高度。
1.满足初稳性要求GM 的极限重心高度
![]()
因为规范要求经自由液面修正后的初稳性高GM应满足:
![]()
![]()
![]() 所以,其极限重心高度为:
所以,其极限重心高度为:
式中 为自由液面对初稳性高的修正值。
2. 满足复原力臂l30、极限静倾角��������m等要求的极限重心高度
先假定几个重心高度,然后根据假定重心高度,排水量及稳性横截曲线求出静稳性曲线。从而可得各个假定重心高度的复原力臂l30、极限静倾角��������m。以复原力臂l30、极限静倾角��������m为纵坐标,假定重心高度为横坐标,绘制如图4-36所示之曲线。
复原力臂曲线l30与量l =0.2m直线交点对应的重心高度即为满足复原力臂量l30要求的极限重心高度zGmax2 。
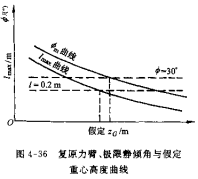 极限静倾角��������m曲线与��������=30o直线的交点所对应的重心高度即为满足极限静倾角��������m要求的极限重心高度zGmax3。
极限静倾角��������m曲线与��������=30o直线的交点所对应的重心高度即为满足极限静倾角��������m要求的极限重心高度zGmax3。
3. 满足稳性核准数K不小于1要求的极限重心高度
根据以上假定的几个重心高度算出相应的初稳性高度:
![]()
按装载情况算出进水角��������E﹑受风面积Af及其形心Z,根据航区进而求出单位风压,并算出风压倾斜力臂lf。然后根据动稳性曲线、横摇角��������0、进水角��������E,确定最小倾覆力臂lq。
以lq为纵坐标,假定重心高度为横坐标绘制如图4-37所示曲线。lq曲线与纵坐标值为风压倾斜力臂lf的水平直线的交点所对应重心高度即为满足K不小于1要求的极限重心高度zGmax4。
在同一排水量下,由以上可算出4个极限重心高度值,显然,最小的那个即为满足所有稳性要求的极限重心高度zGmax。
取若干不同排水量作类似计算,便可获得图4-35不同排水量的极限重心高度曲线。
一、船体几何要素对稳性的影响
1. 干舷高度对稳性的影响
A、B 两种船型,除型深外其它要素和重心高均相同。型深大者的干舷较高。 在倾斜水线未超过A船的甲板边缘时,两者的稳性相同。当超过A船的甲板边缘后,B船的复原力臂较A船大,故B船静稳性曲线的最大复原力臂、极限静倾角及稳距等都较A船为大。增加干舷可有效地改善船的稳性。
2. 船宽对稳性的影响
A、B两种船型,其它要素和重心高均相同。船宽大者水线面惯性矩大,故B船的初稳性高大于A船。另外,船宽大者,出﹑入水楔形的移动力矩也大,因而复原力臂也大。但船宽大者甲板边缘入水角较小,因此B船静稳性曲线的最大复原力臂所对应的横倾角较A船为小。
3. 其他船型要素对稳性的影响
(1)横剖面形状对稳性的影响
A 、B两船,尺度、排水体积和重心高均相同,但A船的横剖面形状是U型,B船的形状是V型,从而B船的水线面系数比A船大,所以B船的初稳性高和复原力臂均比A船大。
(2) 横剖面底部升高对稳性的影响
底部升高的船型,使出水楔形的体积和移动力矩减小导致静稳性臂和稳距的减小。此外,水线以上横剖面的“外飘”和采用较大的舷弧,都可增加倾角较大时的复原力臂。
二、重心位置对稳性的影响
![]() 假设船舶重心在G点时的复原力臂为l,若重心垂直向上移动了一个距离至G1处,则其复原力臂为:
假设船舶重心在G点时的复原力臂为l,若重心垂直向上移动了一个距离至G1处,则其复原力臂为:
如果重心向下移至G2处,则其复原力臂为:
提高重心将使初稳性高、复原力臂和稳距都相应减小。降低重心则作用相反。重心位置对船舶稳性有 重大影响!
三、提高船舶稳性的措施
提高船舶稳性措施有两方面:
提高船舶最小倾覆力矩(或力臂);二是减小所受到风压倾斜力矩(或力臂)
提高最小倾覆力矩有如下的措施:
(1)降低船的重心。设计时要高度重视各种设备和重量的重心高度的布置。在设计或使用时,将船的底部加压载,以降低船舶的重心高度。
(2)增加干舷高度。这是提高船舶初稳性的有效措施之一,某些稳性不足的老船可将载重线降低以增加干舷高度。
(3)增加船宽。这是提高船舶初稳性的有效措施之一,有些老船初稳性不足时,常在船的两舷水线附近加装相当厚的护木和浮箱等,或可在舷侧加装一个凸出体。
(4)注意船舶水线以上的开口和水密性,提高船舶的进水角。
减小风压倾斜力矩有如下的措施:
主要是减小船的受风面积,也就是减小上层建筑的高度和长度。某些小型海洋船舶以及渔轮等,为了保证优良的航海性能,不得不降低船员的生活条件和工作条件,将居住舱室和驾驶室等做得矮小一些。
第五章 抗沉性
§5-1 进水舱的分类及渗透率
一、进水舱的分类
1.第一类舱:舱的顶部位于水线以下,船体破损后海水灌满整个舱室,但舱顶未破损,因此舱内没有自由液面;双层底和顶盖在水线以下的舱柜属于这种情况。
2.第二类舱:进水舱未被灌满,舱内的水与船外的海水不相连通,有自由液面;为调整船舶的浮态而灌水的舱以及船体破洞已被堵塞但水还没有抽干的舱室都属于这种情况。
3.第三类舱:舱的顶盖在水线以上,舱内的水与船外海水相通,因此舱内水面与船外海水保持同一水平面。这种船体破损较为普遍,也是最典型的情况。
二、计算抗沉性的两种基本方法
船舶破损进水后,如进水量不超过10~15%,则可以应用初稳性公式来计算船舶进水后的浮态和稳性,其结果误差甚小。
计算船舱进水后船舶浮态和稳性的基本方法:
1. 增加重量法:把破舱后进入船内的水看成是增加的液体重量;
2. 损失浮力法(固定排水量法):把破舱后的进水区域看成是不属于船的,即该部分的浮力已经损失,损失的浮力借增加吃水来补偿。对于整个船舶来说,其排水量不变,故又称为固定排水量法。
应该指出,用上述两种方法计算所得的最后结果(如复原力矩、横倾角、纵倾角、船舶的首尾吃水等)是完全一致的。但由于两种方法计算的排水量▽不同,它们的横稳性高GM和纵稳性高GML也不同。
由于舱内有各种结构构件、设备、机械和货物,舱内实际进水的体积V1总是小于空舱的型体积V,两者之比成为体积渗透率:

体积渗透率μv的大小视舱室用途及装载情况而定,我国《海船法定检验技术规则》规定的μv的数值加表5-l所示。

面积渗透率:进水面积a1与空舱面积a

![]()
��������v与��������a 之间并无一定联系,通常��������v小于��������a,但并非一定 。在一般计算中,可取��������v=��������a 。
§ 5-2 舱室进水后船舶浮态及稳性计算
一、第一类舱室
对于这类舱室,用增加重量法进行计算比较方便,可直接应用第3章中的有关结论。
如图所示,船在舱室进水前浮于水线WL处,首尾吃水为dF及dA(平均吃水为d),排水量为△,横稳性高为GM,纵稳性高为GML,水线面面积为AW,漂心纵向坐标为xF,进水舱的体积为V,其重心在C(x,y,z)处。可把进入该舱的水看成是在C处增加了重量为p=ωV的液体载荷,且没有自由液面。
二、第二类舱室
舱内的水虽与船外海水不相联通,但因舱室未被灌满,故存在自由液面。在用增加重量法进行计算时,要考虑到自由液面对稳性的影响。
船舶原浮于水线WL处,排水量为△ ,首尾吃水为dF及dA(平均吃水为d),横稳性高为GM,纵稳性高为GML,水线面面积为AW,漂心纵向坐标为xF,进水舱的体积为V,其重心在C(x,y,z)处。可把进入该舱的水看成是在C处增加了重量为p=ωV的液体载荷,进水舱内自由液面对于其本身的纵向主轴和横向主轴的惯性矩分别为ix及iy 。
三、第三类舱室
这类舱室破损进水后,舱内的水面与船外海水保持同一水平面,其进水量需由最后的水线来确定,而最后的水线位置又与进水量有关。因此,用增加重量法进行计算就很不方便。对于这类舱室宜采用损失浮力法来进行计算,并认为舱室进水后船的排水量和重心位置保持不变。
船舶原浮于水线WL 处,排水体积为▽ ,吃水为d,横稳性高为GM,纵稳性高为GML,水线面面积为AW,漂心纵向坐标为xF,进水舱体积为V,其重心在C(x,y,z)处。该舱在WL处进水面积为a,其形心在f(xa,ya) 处,a称为损失水线面面积。
当海水进入该舱后,船舶即损失了浮力ωV,但因船的重量没有改变,故需下沉至W1L1处获得补偿浮力,方能使船舶保持平衡。这样便可按下列步骤进行计算。
四、一组舱室进水的情况
在一组舱室同时破损,将其看成一个等值舱进水,即船舶的浮态及初稳性可根据此等值舱进行计算。首先需要算出此等值舱的有关数据。
(1)等值舱的进水体积
(2)等值舱的重心位置
对于第三类舱室,还需算出:
(3)等值舱在原来水线处的损失水线面面积
(4)等值舱损失水线面面积的形心坐标
将所得到的等值舱数据代人前面的相关公式中。便可算出船舶在一组舱室破损后的浮态和稳性。
§5-3 可浸长度的计算
我国《海船法定检验技术规则》规定:民用船舶的下沉极限是在舱壁甲板上表面的边线以下76mm处,即船舶在破损后至少应有76mm的干舷。
在船舶侧视图上,舱壁甲板边线以下76mm处的一条曲线(与甲板边线相平行)称为安全限界线(简称限界线)。
限界线上各点的切线表示所允许的最高破舱水线(或称极限破舱水线)。
为了保证船舶在破损后的水线不超过此界限,对于舱室的长度必须加以限制。船舱的最大允许长度称为可浸长度。它表示进水以后船舶的破舱水线恰好与界限线相切。破舱在船长方向的位置不同,其可浸长度也不同。
一、计算可浸长度的基本原理
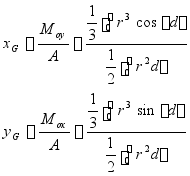
如图:船舶原浮于计算水线WL处,排水体积为![]() ,浮心纵向坐标为
,浮心纵向坐标为![]() 设某舱破损进水后,船舶恰浮于极限破舱水线W1L1处,排水体积为
设某舱破损进水后,船舶恰浮于极限破舱水线W1L1处,排水体积为![]() ,浮心纵向坐标为
,浮心纵向坐标为![]() 若破舱的进水体积为
若破舱的进水体积为![]() ,形心纵向坐标为
,形心纵向坐标为![]()
三、可浸长度曲线的计算
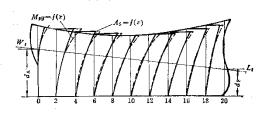
1.绘制极限破舱水线
在邦戎曲线图上,先画出计算水线和限界线,并从限界线的最低点画一条水平的极限破舱水线H。然后在首尾垂线处,自H线向下量取一段距离z,其数值可按下式估算:
z=1.6D-1.5d
其中D-舱壁甲板的型深,d-吃水,在距离z内取2~3个等分点。
并从各等分点作与限界线相切的纵倾极限水线1F,2F,3F,1A,2A,3A等。
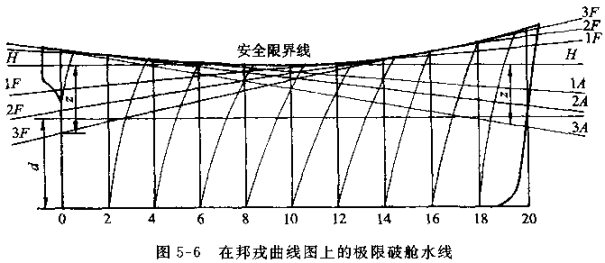
通常极限破舱水线约取7~10条,其中尾倾水线3~5条,水平水线1条,首倾水线3~4条。这些破舱水线对应于不同舱室进水时船舶的最大下沉限度。
2.计算进水体积及纵向坐标
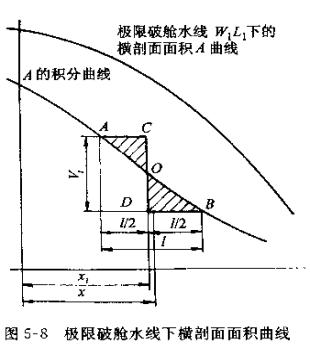
在邦戎曲线上,分别量取计算水线及破舱水线的各站横剖面面积,并用数值积分法分别计算出相应于计算水线和极限破舱水线的排水体积▽和▽1,以及对于中横剖面的体积静矩M和M1,即可求得破舱的进水体积Vi及形心纵向坐标xi ,计算各破舱水线下的进水体积Vi及形心纵向坐标xi,绘制Vi- xi曲线。
3.计算进水舱的可浸长度
设某极限破舱水线W1L1处的破舱进水体积为Vi,其形心纵向坐标为xi。现在的问题是如何求出船舱的长度和位置,当该舱破损后,进水体积正好为Vi ;面形心纵向坐标恰好又在xi处,对于这种计算用图解法较为简便。
如图:先画出极限破舱水线W1L1在xi附近一段的横剖面面积曲线及该段的积分曲线,然后,在xi处作一垂线与积分曲线相交于O点,在该垂线上截取CD=vi,并使面积AOC=BOD,则A点和B点间的水平距离为可浸长度l。同时该舱中点至中横剖面的距离x也可在该图上量取。
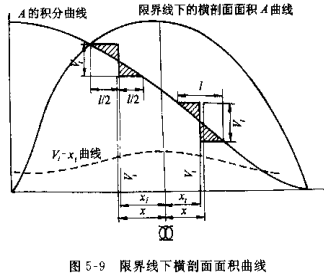
应用同样方法,可以求出各极限破舱水线的舱室可浸长度及其位置,但这种方法需要绘制每一破舱水线的横剖面面积曲线及其积分曲线,因而计算和制图工作过于繁杂。
实践证明:进水舱的位置通常总是在其相应破舱水线与限界线相切的切点附近,故破舱水线下的横剖面面积曲线与限界线下的横剖面面积曲线在进水舱附近几乎相同。因此在实际计算中,常用限界线的横剖面面积曲线及其积分曲线来代替所有破舱水线的横剖面面积曲线及其积分曲线,如图所示。这样便可以迅速求出所有破舱水线的进水舱长度及位置。
在进水舱附近,限界线下的横剖面面积略大于破舱水线下的横剖面面积,故计算所得之可浸长度略小于实际长度,偏于安全方面,因此是允许的。
可浸长度的实际近似计算法
1)求安全界限下的横剖面面积A曲线
2)求A的积分曲线
3)在A的积分曲线上,求可浸长度。
4.绘制可浸长度曲线
根据算得的各进水舱的可浸长度及其中点至中横剖面的距离,在船体侧视图上标出各进水舱的中点,并向上作垂线,然后截取相应的可浸长度为纵坐标并连成曲线,即得可浸长度曲线。
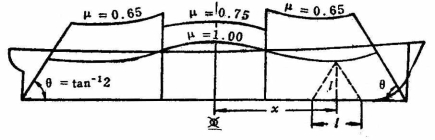
由此所得的可浸长度系假定进水舱的渗透率μ=1.0,事实上各进水舱的μ总是小于1.0的,故在图中还需画出实际的可浸长度曲线,并注明μ的具体数值。可浸长度曲线的两端,被船舶首尾垂线处θ=arctan 2的斜线所限制。
§5-4分舱因数及可浸长度
船舶的抗沉性是由水密舱壁将船体分隔成适当数量的舱室来保证的。如果只用可浸长度曲线来检验船舶横舱壁的布置是否满足抗沉性要求,那就未免过于粗略,因为它不能体现出各类船舶在抗沉性方面要求的不同。为此,在《海船法定检验技术规则》中采用了一个分舱因数F来决定许用舱长。F是一个等于或小于1.0的系数,即F≤1.0。这样有
许可舱长=可浸长度×分舱因数=l × F
将实际的可浸长度曲线乘以分舱因数F后,使得到许用舱长曲线,如上图所示。
假定水密舱壁的布置恰为许用长度,这时:
当F=1.0时,许可舱长等于可浸长度,船在一舱破损后恰能浮与极限破舱水线而不致于沉没;
当F=0.5时,许可舱长等于可浸长度的一半,船在相邻两舱破损后恰能浮于极限破舱水线处;
当F=0.33时,许可舱长等于可浸长度的1/3,船在相邻三舱破损后恰能浮与极限破舱水线处。
如果船舶在一舱破损后的破舱水线不超过限界线,但在两舱破损后其破损水线超过限界线,则该船的抗沉性只能满足一舱不沉的要求,称为一舱制船;相邻两舱破损后能满足抗沉性要求的船称为两舱制船;相邻三舱被损后仍能满足抗沉性要求的船则称为三舱制船。若用分舱因数F来表示,则:
对于一舱制:1.0≧F>0.5
对于二舱制:0.5≧F>0.33
对于三舱制:0.33≧F>0.25
因此,分舱因数F是决定船舶抗沉性要求的关键因素,其具体数值与船长、用途和业务性质有关,在规范中有详细规定。
船舶水密舱的划分,是根据实际需要而布置的。许用舱长曲线仅作为保证船舶满足抗沉性的要求,而对舱的长度加以一定的限制。若实际舱长小于或等于许用舱长,则船舶的抗沉性满足要求。
最后应该指出:在上述可浸长度和许用舱长的计算中,没有考虑破舱后的稳性问题。故尚需对稳性进行校核计算。对于一舱制船舶,应计算任一舱室进水后的稳性;对于二舱制船舶,应计算任意两个相邻舱室同时进水后的稳性;对于三舱制船舶,则应计算任意三个相邻舱室同时进水后的稳性。
船舶破损后对稳性的要求
《规范》对国际航行单体客船的破舱稳性要求是:船舶破损后(若为不对称舱进水,但已采取平衡措施)其最终状态应满足:
(1)用损失浮力法计算的初稳性高应不小于0.05m。
(2)不对称进水情况下,一舱进水的横倾角不得大于7o。两个或两个以上相邻舱进水后,横倾角不得超过12o。
(3)在任何情况下,船舶最终破舱水线的最高位置不得超过界限线。
(4)正值的剩余复原力臂不得小于0.10m,且在平衡角以后应有一个15o的最小范围。
(5)从平衡角到进水角或消失角(取小者)之间正值范围的复原力臂曲线的面积应不小于0.015m·rad。
§5-5 客舱分舱和破舱稳性计算
旧的安全公约:要求船舶设置一定数量的水密舱,使船破损后的浸水限制在一定的范围内,以此保证船舶在一舱或数舱破损后,其水线不超过限界线并具有一定的破舱稳性。
但船舶在海上破损具有很大的随机性,因此应用概率计算方法研究船舶的抗沉性更为合理。
从1962年,政府间海事协商组织(IMCO:Inter-Government Maritime Consultative Organization)的分舱、稳性和载重线分委员会开始收集资料,着手准备以概率论为基础的新的衡准方法。
1973年IMCO第八届大会A.265决议通过新的衡准规则,即《国际航行客船的分舱与稳性规则》,1980年5月该规则正式生效。我国承认新、旧两个规则。
国际航行货船的分舱和破舱稳性概率方法计算规则也于1992年2月1日起生效。
在制订等效新规则时,遵循了如下原则:
(1)新规则的安全程度应大体与原来安全公约要求相当。
(2)船舶的安全程度随船长和旅客的增加而提高。
(3)采用分舱指数作为衡量船舶在破损后具有残存能力的安全程度的衡准。这一指数应反映出舱壁间距、稳性以及其它一些有关特征对残存能力的影响。
新规则的主要特点是采用概率计算方法。对一艘破损的船舶能否残存,是由大量的随机因素决定的。破损对船舶的影响取决于:哪一个舱或相邻一组舱进水;破损时船舶的吃水及完整稳性;破损处所的渗透率以及破损时的海况等因素。这些因素之间的关系及其影响随不同情况而变化,因此只能以概率作为比较基础,用一些近似的办法或定性的判断,对船舶的安全进行估计和校核。
新规则制订的基础是:
(1)对实船的海难资料作破损统计,得出破损范围(长度、深度)及位置的分布函数,再求得某一舱或舱组进水概率的计算公式。
(2)以模型试验及船舶碰撞时的海况报告为基础,得出某一舱或舱组进水后,船舶不致倾覆或沉没的概率计算公式。
(3)最后,船舶破损后残存概率就等于进水概率乘以不致倾覆或沉没的概率之总和。
二、主要衡准
(1)分舱
所有舱室应保证一舱不沉,但对船长LS≥100 m的船,首尖舱和其相邻舱组成的舱组应满足两舱不沉,对N>600的船舶应保证自船长前端量起的长度范围内两舱不沉。
这里:Ls为船舶分舱长度,指船舶在淹没限界线以下部分的最大型长,即上甲板的后缘至前缘总长;
N=N1+2N2
其中:N1为备有救生艇的人数,N2为船舶准予搭载多于N1的人数,包括船员。
新规则明确规定船侧的破损范围及位置:
①横向范围=0.2B1,B1为最深分舱载重线(或其下)船
长中点处的最大船宽。
② 纵向范围=3m十0.03LS或11 m,取小者。
(a)破损可发生在船长方向的任何位置,但不包括横舱壁,若舱壁有台阶时,应假定其遭受破损。
(b)对N>600的船舶,自LS前端量起,在长度范围内任何位置发生船侧破损时,应包括横舱壁在内。
③垂向范围:自基线向上不受限制。
④若垂向、横向、纵向较小范围的浸水导致要求更高的完整稳性,则应假定此范围破损,并且此时船壳只有一个破口和一个自由液面。
⑤冷藏处所的舱壁和甲板被看作是限制进水的,未破损的水密分隔结构亦被看作是限制进水的。
(2)稳性和浮性
①在进水最终阶段:
(a)用固定排水量法对船舶正浮状态算出的初稳性 ![]() (m)应不小于下列各式计算所得的最大值:
(m)应不小于下列各式计算所得的最大值:
![]()
式中:B 2为有关舱壁甲板的船长中点处的最大型宽(m);Δ为船舶未破损时的排水量(t);F1为有效平均破损干舷,等于船舶正浮情况下,在有关舱壁甲板和破损水线间,船长中点前 1/3LS和后1/3LS间这部分投影面积除以2/3LS
(b)一舱进水时的横倾角不得超过70;两个或两个以上的相邻舱同时进水时横倾角不超过120。
(c)除进水舱或舱组外,有关舱壁甲板的甲板边线的任何部分均不应该被淹没。
②在平衡前及进水中间阶段:
(a)平衡前(若不对称舱进水、但未采取平衡措施)及进水中间阶段的最大横倾角不得超过200,且不得导致继续浸水。
(b)剩余稳性是足够的。
(c)若需设置平衡装置,则这些装置尽可能为自动,且应能在最高有关甲板以上进行操纵控制,而且其使船平衡的时间不得超过10分钟。
(3)船舶达到的分舱指数A应不小于要求的分舱指数R,即
A≥R
满足此要求的船是合格的,否则不合格。
三、要求的分舱指数
船舶的分舱程度由下式所要求的分舱指数R来确定:
![]()
N=N1+2N2
若按N=Nl十2N2计算不能满足主要衡准要求时,则可取满足N1+N2<N<N1+2N2的N,但必须得到主管机关认可。从R表达式可见,船舶所要求的安全程度随LS和N的增大而提高。
四、达到的分舱指数
达到的分舱指数A就是船舶破损后的残存概率。
![]()
![]() 式中:a为在船长方向LS范围内的舱室纵向位置对被损概率的影响因数;p为纵向破损长度对某一舱或舱组可能进水概率的影响因数;S为某一舱或舱组进水后的残存概率,即最终进水状态时干舷、稳性和横倾的影响因数; 为表示在船舶长度上取每个舱或舱组单独计算而得的总和。
式中:a为在船长方向LS范围内的舱室纵向位置对被损概率的影响因数;p为纵向破损长度对某一舱或舱组可能进水概率的影响因数;S为某一舱或舱组进水后的残存概率,即最终进水状态时干舷、稳性和横倾的影响因数; 为表示在船舶长度上取每个舱或舱组单独计算而得的总和。
由A表达式定义可知,a、 p表示某一舱或舱组破损进水的概率,S是表示某一舱或舱组进水后不致倾覆和沉没的概率。
关于a、p、S的具体计算,可参阅有关规则及资料。
按新规则计算客船的分舱和破舱稳性相当繁复,工作量很大,现都用计算机进行计算。
第6章 船舶下水计算
§6-1 概述
一、下水定义
船舶在船台上或船坞内建造到一定程度后便可下水,即将原在船台上或船坞内呈支撑状态的船进入水中呈漂浮状态。
二、下水方式
1、起重机吊:小船造好后可以用起重机把它吊到水中
2、造船坞下水:船在船坞内建造,造好后向船坞内放水使船浮起再拖到船坞外的水域中。造船坞是目前解决大型船舶建造和下水的较好设施。
3、船台重力下水:即船舶在本身重力的作用下沿船台倾斜滑道滑入水中,是常用的下水方法。主要包括纵向下水和横向下水两种。
(1)纵向下水:船体的中纵剖面平行于滑道运动。
(2)横向下水:船体的中横剖面平行于滑道运动。
鉴于我国各主要船厂普遍采用纵向下水方式,故在本章中只限于讨论船舶纵向下水的计算。
三、纵向下水布置概述
1、下水设备
(1)固定部分:固定部分由木方铺成,称为滑道。
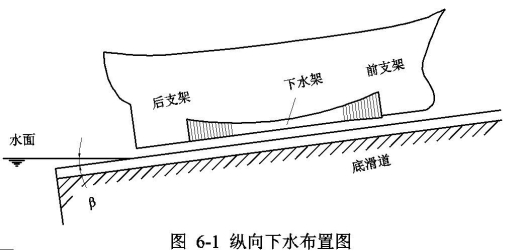
滑道通常采用两条,其中心线之间的距离约为船宽的1/3。
滑道坡度β一般取为1/12-1/24,其具体数值视船的大小而定:
小型船舶(船长100m以下): β= ![]()
中型船舶(船长100m~200m):β= ![]()
大型船舶(船长200m以上): β= ![]()
大船的滑道坡度一般较小,以免船首部分离地过高,影响施工,船的龙骨坡度α与滑道坡度β大体相同,有时α较β约小 ![]() 。
。
(2)运动部分
运动部分在下水过程中与船舶一起滑入水中,称为下水架。
下水架的底板称为滑板,在滑板与滑道之间敷有润滑油脂,使滑板易于滑动。
下水架的两端比较坚固,以支持船体首尾两端的尖削部分,分别称为前支架及后支架。
![]() 下水架的长度约为船长的80%,船体首尾两端各有10%左右的长度悬空于下水架之外。
下水架的长度约为船长的80%,船体首尾两端各有10%左右的长度悬空于下水架之外。
![]()
![]() 滑板的支承总面积: ( :下水时总重量;P:润滑油脂的许可平均压力)
滑板的支承总面积: ( :下水时总重量;P:润滑油脂的许可平均压力)
滑板宽度: (l:下水架长度;n:滑道数目)
(3)辅助设备
套牢装置:防止船在开始下水之前滑板可能滑动
导向挡板:防止船在下水过程中滑板发生偏斜
制动装置:使船在下水后能迅速停止于预定位置
驱动装置:使船在开始下水时能迅速滑动
§6-2 下水阶段划分
一、第一阶段
(1)自船舶开始下滑至船体尾端接触水面为止。
(2)运动特点:平行于滑道运动。
(3)受力分析:
下水重量Wc:其中包括船体重量及下水架重量。重力 Wc沿滑道方向的分力即为下滑力![]() ,垂直于滑道的分力为(正压力)
,垂直于滑道的分力为(正压力)![]() ,如图6-2所示。
,如图6-2所示。
滑道的反作用力R: R与 Wc 在同一作用线上,两者大小相等方向相反。
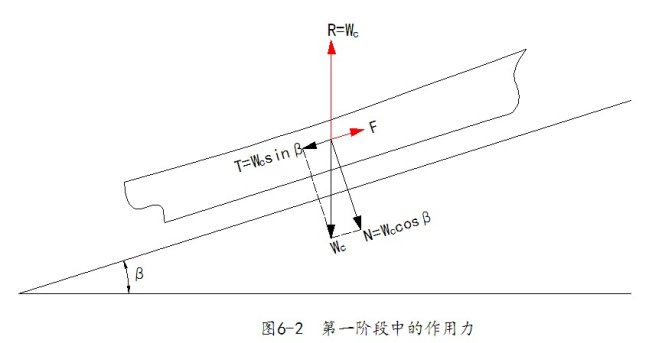
摩擦力 ![]() ,
,![]() 为摩擦系数,其数值与润滑油脂的性质及温度有关。
为摩擦系数,其数值与润滑油脂的性质及温度有关。![]() 又分为静摩擦系数
又分为静摩擦系数![]() (船在开始滑动时)和动摩擦系数
(船在开始滑动时)和动摩擦系数![]() (船在滑道上运动时),通常
(船在滑道上运动时),通常![]() 的数值为:
的数值为:
![]()
![]()
滑动条件
舶在本身重力作用下沿滑道滑动的条件是:
![]()
或
![]() (6-1)
(6-1)
二、第二阶段
(1)自船体尾端接触水面至船尾开始上浮为止。
(2)运动特点:船的运动仍平行于滑道。
(3)受力分析:作用力有:
船体下水重量![]()
浮力![]() (其中
(其中![]() 为船舶入水部分的排水体积);
为船舶入水部分的排水体积);
滑道的反作用力R 。设下水重量![]() 、浮力
、浮力![]() 及反作用力R的作用点至前支架端点的距离分别为
及反作用力R的作用点至前支架端点的距离分别为![]() 、
、![]() 、及
、及![]()
(见图6-3)则在该阶段中力及力矩的平衡方程式为:
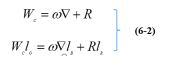
![]()
![]() 反作用力:
反作用力:
反作用力距前支点的距离:
尾下落
当船的重心G已在底滑道末端之后,而船尾尚未浮起
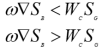 条件: 发生尾下落(见图6-4)
条件: 发生尾下落(见图6-4)
不发生尾下落
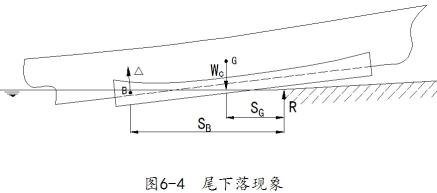
避免措施
增加滑道水下部分的长度;
在船首部分加压载重量,使重心G向船首移动,减小重量对滑道末端的力矩;![]()
增加滑道坡度![]() ;
;
等待潮水更高时下水。这相当于增加滑道水下部分的长度
三、第三阶段
(1)自船尾开始上浮至下水架滑板前端离开滑道为止
(2)运动特点:船舶不再沿平行于滑道的方向移动,下水架的滑板只有前支点与滑道相接触。
(3)上浮条件:当船尾开始上浮时,下水架滑板前端成为支点,因而船尾开始上浮的条件必然是:![]()
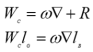 (4)受力特点:①
(4)受力特点:①
② (6-3)(见图6-5)
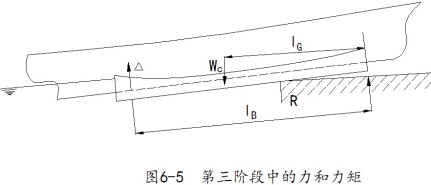
(5)不利情况:
①滑道反力R集中作用于下水架前支点处,可能损坏下水设备及船体结构;
②当船舶绕前支点转动时,首柱底部可能撞击船台,损坏船首结构和船台。
(6)避免方法:
①加强前支架处的结构,并使反力平均作用于前支架之全体;
②取消前支架,在滑板与船体之间的相当长度内只需填入普通楞木,这些楞木随船体及滑板一起下水;
③在船尾上浮处的前支架下方的滑道结构给予适当加强
④两滑道后端的中间挖一凹槽,以免船首底部碰触船台
四、第四阶段
(1)自下水架前支点离开船台滑道至船舶停止运动为止
(2)运动情况:
①船已完全浮起;
②船舶的下水重量仍大于浮力,则将发生船首下落现象,下水重量与浮力之差称为下落重量。
(3)下落高度t:前支架离开滑道末端时的水线与船在自由浮起时首吃水之差。
(4)首沉深度t´������
当船首下落至静止水线时,因有惯性作用,船首将继续下沉,在首垂线处下沉的最深水线与静止水线之距离t´������称为首沉深度,通常t´������=1.1t。
(5)避免措施:
①增加滑道入水部分的长度;
②等待潮水更高时下水;
③中心凹槽;
④在滑道末端增加河床深度。
(6)下水船舶在离开滑道之后,由于惯性作用将继续向前滑动,故应采取适当措施使船停止运动。
①抛锚;
③ 制动;
④ 在舵的后面绑一块横向木板。
§6-3 下水曲线计算
一、下水曲线图
(1)组成(见图6-8)
![]() 下水重量 =常数(水平直线);
下水重量 =常数(水平直线);
![]()
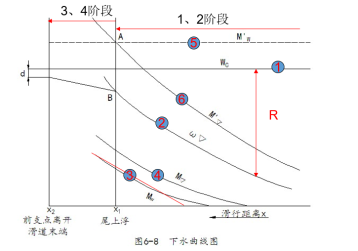 浮力 (曲线);
浮力 (曲线);
下水重量对于滑道末端的力矩
![]() (倾斜直线);
(倾斜直线);
浮力对于滑道末端的力矩
![]() (曲线);
(曲线);
下水重量对于下水架前支点的力矩
![]() 常数(水平直线);
常数(水平直线);
浮力ω▽对于下水架前支点的力矩
![]() (曲线)。
(曲线)。
(2)特点
①下水重量![]() 与浮力ω▽曲线之差即为船在不同行程时滑道的反力R。
与浮力ω▽曲线之差即为船在不同行程时滑道的反力R。
② ![]() 直线与
直线与![]() 曲线的交点(A点)表示船尾开始上浮,与之相应的
曲线的交点(A点)表示船尾开始上浮,与之相应的![]() 表示船尾开始上浮时的行程数值。
表示船尾开始上浮时的行程数值。
③若![]() 曲线位于
曲线位于![]() 曲线之上,则
曲线之上,则 ![]() ,不发生尾下落现象,反之,发生尾下落。
,不发生尾下落现象,反之,发生尾下落。
④第三阶段,其浮力随行程的变化规律与一、二阶段不同,设行程![]() 表示下水架前支点已离开滑道末端,若
表示下水架前支点已离开滑道末端,若 ![]() ,则将发生首下落现象,其差数d即为首下落重量。
,则将发生首下落现象,其差数d即为首下落重量。
二、下水计算
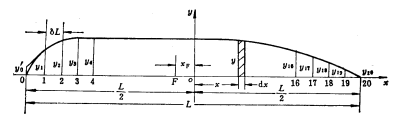
(1)根据第二章中关于重量及重心计算的基本原理,尽可能正确地计算下水重量及重心位置;
(2)绘制如图6-9所示的下水布置图,并注明有关尺寸;

(3)确定船舶滑行某一距离x时的首尾吃水;
![]()
(L为船舶垂线间长,α为龙骨坡度,β为滑道坡度)
根据上式可以把船在各不同行程 ![]() (例如:x=60m、80m、100m等)时的首尾吃水算出。
(例如:x=60m、80m、100m等)时的首尾吃水算出。
(4)在邦戎曲线图上画出相当于上述不同行程x时的水线,然后用数值积分法算出每一水线下的浮力ω▽及浮心纵向位置,据此可求出 ![]() 及
及![]() ,也可得出不同行程x时的ω▽、
,也可得出不同行程x时的ω▽、![]() 、
、![]() 数值。根据下水重量及重心位置,可算出
数值。根据下水重量及重心位置,可算出![]() 及
及 ![]() 。
。
(5)绘制下水曲线图,由 ![]() 确定船尾开始上浮的位置
确定船尾开始上浮的位置![]() 。
。
(6)计算船尾上浮以后的浮力、绘制曲线(见图6-11)
① 先选定某一![]() 值(
值(![]() ),计算船舶在前支点处的吃水;
),计算船舶在前支点处的吃水;
② 假定若干个尾吃水,在邦戎曲线上画出这些水线,并量出各横剖面面积;
③ 应用数值积分法算出ω▽、浮心位置、![]() ;
;
④以尾吃水为横坐标,绘制浮力ω▽曲线、![]() 曲线及
曲线及![]() 直线;
直线;
⑤在![]() =
=![]() 处得对应尾吃水,对应的浮力ω▽也可查得;
处得对应尾吃水,对应的浮力ω▽也可查得;
⑥同理假定另外几个x值,可确定每个x下对应的ω▽;
⑦绘制下水曲线中![]() 阶段的浮力曲线。
阶段的浮力曲线。
(7)为了估计船在入水后的浮态及稳性,尚需计算船舶下水后的首尾吃水及初稳性高。
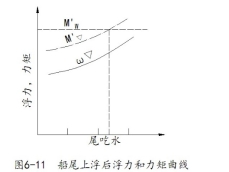
§6-4 滑道压力计算
为了保证船舶安全下水,还应对滑道压力进行计算,以便检验润滑油脂、滑道及前支架是否能承受该项压力。船舶在下水过程中,滑道上的受力情况是变化的,故对压力计算也需分阶段进行。
一、下水第一阶段
(1)受力:整个下水重量完全由滑道支承,滑道的反力R等于下水重量![]() ,即
,即
![]() =R
=R ![]() (6-5) (式中: 为下水船舶重心G至滑板前端的距离; 为滑道反力R的作用点至滑板前端的距离)
(6-5) (式中: 为下水船舶重心G至滑板前端的距离; 为滑道反力R的作用点至滑板前端的距离)
(2)压力分布及大小
8W4[GJ_HC](76fc163c-6f05-4f10-ba5d-38d057460a41_8630084.967.jpeg)
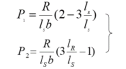 设:滑道压力沿滑道长度按梯形分布(见图6-12),则
设:滑道压力沿滑道长度按梯形分布(见图6-12),则
(6-7)
(其中:b为每条下水滑道的宽度,![]() 、
、![]() 分别为滑板前端和后端处滑道所受的压力)
分别为滑板前端和后端处滑道所受的压力)
二、下水第二阶段
![]() (1)受力:当下水进入第二阶段时,船体受到浮力的作用,这时滑道反力R及其作用点至前支点的距离
(1)受力:当下水进入第二阶段时,船体受到浮力的作用,这时滑道反力R及其作用点至前支点的距离![]() 可由下式决定:
可由下式决定:
(6-8)
(2)压力分布及大小:与R的作用点的位置有关
①当反力R作用点位于滑道接触长度中央的![]() 的范围内
的范围内
(即![]() )时,滑道压力为梯形分布(见图6-12),
)时,滑道压力为梯形分布(见图6-12),
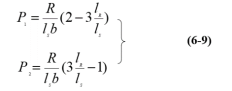 则前端及后端滑道处所承受的压力为:
则前端及后端滑道处所承受的压力为:
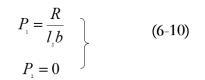 ②当反力R的作用点至前支点的距离
②当反力R的作用点至前支点的距离![]() 时,则滑道压力为三角形分布(见图6-13),前端及后端处滑道所承受的压力为:
时,则滑道压力为三角形分布(见图6-13),前端及后端处滑道所承受的压力为:
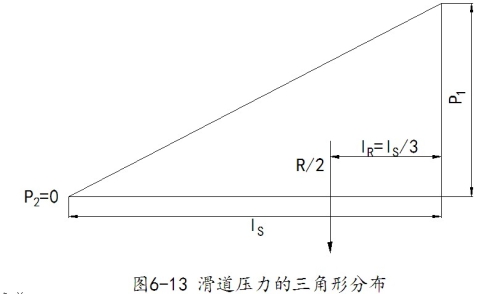
③当反力R的作用点至前支点的距离![]() 时,因滑板与滑
时,因滑板与滑
![]() 道之间不能承受拉力,故两者之间的有效接触长度:
道之间不能承受拉力,故两者之间的有效接触长度:
滑道压力沿有效长度 的分布如图6-14所示,前端及后端处
 滑道分别承受的压力:
滑道分别承受的压力:
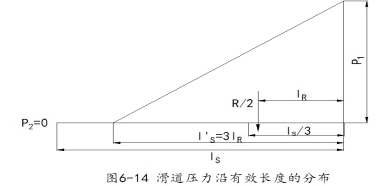
(4)当船尾开始上浮时,反力R集中作用于滑板前端。设前支架处平均受压的长度为 ![]() ,则船尾上浮时该处滑道所受的压力
,则船尾上浮时该处滑道所受的压力
![]()
第7章 船舶阻力概述
第1节 船舶快速性及其在船舶设计中的地位
1.1 船舶快速性的含义
快速性的概念并不是指的绝对航速的高低
在给定功率时,使航速较高Resistance
在给定速度时,船舶尽可能消耗较小的主机功率Propulsion
1.2 研究内容和任务
各阻力成分的成因及其性质
阻力随航速、船型和外界条件的变化规律
减小阻力的方法,寻找优良船型
估算船舶阻力,为推进器设计提供依据
1.3 研究方法
理论研究方法
流体力学基本理论
试验方法
船模试验
实船试验
数值模拟 (CFD)
信息量大,成本低,易并行化,快速响应
试验方法:
船模试验:按照相似理论制作小尺度的船舶和桨 模,在拖曳水池中进行试验,观察并记录相关数据,经过分析可以对快速性进行预估,是不可或 缺的研究手段。
存在固有的局限性
实船试验:用于鉴定船舶的各种性能是否能达到 设计标准,并同船模试验比较,分析尺度效应的 影响,验证船模试验结果的准确性。
第2节 船舶阻力的成因及分类
2.1 船舶航行中的阻力
船舶阻力:船舶航行时受到的与船体运动方向相反的力
常用阻力划分:Rt=Rf+Rvp+Rw
船体总阻力 Rt Total resistance
粘性阻力 Rv Viscous resistance
兴波阻力 Rw Wave-making resistance
摩擦阻力 Rf Frictional resistance
粘压阻力 Rvp Viscous pressure resistance
压阻力 Rp Pressure resistance
2.2 阻力成分的主要特性
阻力各成分随速度变化的速度不同。
船型给定时,外界条件不变的前提下,船体阻力可以看做仅仅是船速Vs的函数。
小结:影响阻力的因素有速度、船型、介质(水)运动粘性系数。
第3节 阻力相似定律
3.1 力学相似
几何相似Geometric Similitude
两个物理系统任意对应线性比例尺度为一常数:
![]()
![]()
运动相似Kinematic Simlitude
两个物理系统任意点时间比为一常数:![]()
几何相似和运动相似可推出:![]()
两物理系统任意对应速度之比为一常数![]()
两物理系统任意对应加速度之比为常数
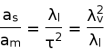
动力相似Dynamic Similitude
两个物理系统任意对应力之比为一常数 ![]()
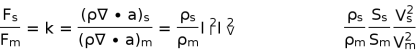
用动压力![]() 代替
代替![]()
![]()
若实船与船模力学相似,则各阻力系数相等
3.2傅汝德定律——兴波阻力相似定律
分析前提:实船与船模仅受重力作用
假定船舶在理想流体中运动,此时仅有重力引起的Rw
重力之比等于惯性力之比:![]()
令![]()
![]()
得到 ![]()
![]()
仅在重力作用下,力学相似条件为Frs=Frm
傅汝德相似定律应用
形似船在相应速度时的兴波阻力系数相等
形似船:几何相似船的统称,如实船与船模
相应速度:形似船Fr相等时,其速度存在一定关系
Frs=Frm![]()
兴波阻力是重力引起的阻力,实船与船模在相应速度时兴波
阻力系数相等
![]()
傅汝德相似定律应用
Fr相等时,形似船的单位排水量的兴波阻力相等
即满足傅汝德比较律:![]()
![]()
3.3 雷诺定律——粘性阻力相似定律
![]() 分析前提:
分析前提:
![]() 实船与船模仅受粘性力作用。
实船与船模仅受粘性力作用。
注意:实船与船模雷诺数相等条件Rem=Res 难以实现。
3.4 全相似定律——总阻力相似定律
分析前提:同时考虑兴波和粘性的影响。
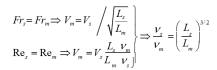
注意:在目前条件下,船模与实船的全相似 无法满足,船模试验只能在部分相似条件下 进行,即满足Froude相似条件。
第8章 粘性阻力
第1节 粘性阻力与边界层
1.1 边界层理论
流体粘性的成因:
① 流体分子间的相互碰撞
② 分子间具有内聚吸引力
使得流体流经物体表面时,被粘附与物理表面之上
在雷诺数较大的情况下,流体的粘性主要表现在靠近物体表面很薄的流体层中,这一薄层称为边界层
边界层概念的提出:
1904年由普朗特提出,是流体力学的里程碑
边界层理论的意义在于将流体划分为截然不同两个部分加以处理:
① 边界层外:理想流体,势流理论
② 边界层内:真实流体,边界层理论
1.2 平板边界层
流动特点:
① 随流体向前运动,速度受到影响的区域逐渐扩大
② 随与物体法向距离,物体对流体的减速作用逐渐减弱
③ 在离平板一定距离(y=δ)之外,流体速度基本不受物体影响,此时流体速度u=均匀来流速度ue
④ 重要特征:
1、边界层外缘、边界层厚度的界定(99%U)
2、界层内速度是变化的,沿界层厚度方向存在速度梯度
3、 沿界层厚度方向的压力不变![]()
边界层外缘的压力=物面上的压力
界层内的流动随局部雷诺数不同而不同Rex=![]()
边界层内流动状态 local Reynolds number
层流状态
过渡区(转捩点)
湍流状态(紊流状态)
层流底层(粘性底层)

1.3 船体边界层
基本特征:
① 船体几何形状十分复杂,有纵向和横向曲率,相应其边界层为三维边界层(非二维)
② 边界层外缘势流与平板势流不同:存在纵向速度梯度、压力梯度,尤其首尾显著
③ 边界层内压力分布不同
④ 船前75%-80%L为薄边界层,之后边界层变厚。
第2节 摩擦阻力的成因与主要特性
2.1 摩擦阻力的成因
平板表面切应力
 平板摩擦阻力
平板摩擦阻力
局部摩擦阻力系数
平均摩擦阻力系数
2.2 摩擦阻力的主要特性
流态的影响:
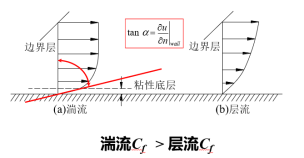
Re的影响:
![]()
![]()
![]()
![]()
![]() 固定流态下,摩擦切应力
固定流态下,摩擦切应力![]() 随局部雷诺数
随局部雷诺数![]() 变化而变化
变化而变化
① ![]() 不变,x增大:
不变,x增大:![]()
![]()
![]()
![]()
![]()
② x不变,![]() 增大:
增大: ![]()
![]()
![]()
![]()
![]()
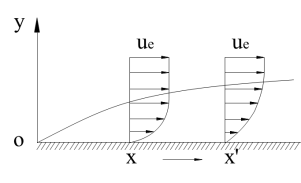

S的影响:
流体介质给定,![]() 为常数
为常数
固定流态下,速度法向导数![]()
![]()
![]() dS
dS ![]() S
S
结论:给定介质流体,固定流态下,![]()
![]() S
S
光滑平板层流摩擦阻力公式
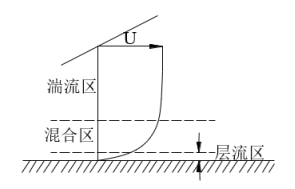 光滑平板湍流摩擦阻力公式
光滑平板湍流摩擦阻力公式
Karman边界层动量积分
常见速度分布形式
湍流边界层多层结构模式
层流段、过渡区的影响
Re较大,湍流系数公式OK
Re较小,需要进行修正
船体摩擦阻力计算的处理方法
Froude相当平板假定
相当平板:与实船或船模同V、L、S的光滑平板
尺度效应:由于模型与实船(或实桨)之间的绝对尺度不同,且 不能同时满足全相似定律,因而引起某些力、力 矩或压力系数甚至流态等性能方面的差别,这种 差别称为尺度效应或尺度作用。
忽略了实际船体与光滑平板的差别:弯曲度、粗 糙度
2. 4 船体表面弯曲度对摩擦阻力的影响
船体表面弯曲度对Rf的影响
物理本质:边界层形成→速度梯度→ Rf
纵向曲率对Rf的影响: Rf ↑
横向曲率对Rf的影响: Rf ↑
边界层分离的影响: Rf ↓( Rvp ↑)
小结:
总体上看,影响并不显著,可用“相当平板”计算
改变船体曲线以减小摩擦阻力收效甚微
粘性应力切向分量与法向分量对曲度的敏感程度完全 不同(设计权衡)
•�������� 船体形状效应的修正
– 形状效应
– 史高斯理论计算分析
•�������� Rf弯曲> Rf平板,且随T/C(弯曲度)增大而增大;
•�������� δ Rf / Rf平板与Re无关
– Rf船体> Rf平板,但是增量较小
– 一些修正方法
•�������� 汤恩公式:![]()
•�������� 形状效应修正因子 ![]() :
:![]()
2. 5 船体表面粗糙度对摩擦阻力的影响
•�������� 船体表面粗糙度对摩擦阻力的影响
– 船体表面粗糙度对Rf的影响既显著又敏感 (10%~30%)
– Q:是否物体表面越光滑,阻力性能就越好呢?
•�������� 有些物体为了减阻,反而可以弄成“粗糙”表面。
•�������� 粗糙度种类
– 普遍粗糙度(漆面粗糙度)
•�������� 常用的粗糙度参数:表面突起高度的统计量。
•�������� 米哈伊洛夫漆面平板阻力试验(三个阶段)
•�������� 水力光滑阶段
•�������� 过渡阶段
•�������� 完全粗糙阶段
•�������� 船模不计粗糙度影响
– 局部粗糙度(结构粗糙度)
•�������� 局部粗糙度对Rf 的影响要小于普遍粗糙度的影响
•�������� 粗糙度种类
– 污底:锈蚀、海草、贝类等(80%)
•�������� 与航行季节(温度)、航区以及出坞后的时间有关
•�������� 解决方法:涂防污漆(环境污染);淡水港停泊(死亡脱落);定期入船坞除污,重新油漆。
现代方法:高分子聚合物防污(环境污染)
![]() •�������� 粗糙表面摩擦阻力计算的处理方法
•�������� 粗糙表面摩擦阻力计算的处理方法
– 粗糙度补偿系数
![]() •�������� 认为DCf =const不随Re变化(米哈伊洛夫;Todd;实船)
•�������� 认为DCf =const不随Re变化(米哈伊洛夫;Todd;实船)
•�������� 我国采用DCf =0.0004,Cf 一般采用1957ITTC公式:
![]() •�������� 实际数据表明DCf 随L而变,1975ITTC建议公式:
•�������� 实际数据表明DCf 随L而变,1975ITTC建议公式:
– “粗糙度补贴系数”
•�������� 阻力:表面粗糙度、不同摩擦阻力公式、尺度作用等
•�������� 推进:螺旋桨效率、伴流、推力减额、相对旋转效率 等
2.6 船体摩擦阻力的计算步骤
![]() •�������� 计算雷诺数:
•�������� 计算雷诺数:
![]() •�������� 计算光滑平板摩擦阻力系数:
•�������� 计算光滑平板摩擦阻力系数:
![]() •�������� 决定粗糙度补贴系数:
•�������� 决定粗糙度补贴系数:
•�������� 计算湿表面积
•�������� – 型线图、经验公式、图谱公式
![]() •�������� 根据公式计算Rf :
•�������� 根据公式计算Rf :
第3节 减少摩擦阻力的方法
3.1 传统方法
•�������� 1) 使湿表面积减少( S↓ )
– 方法:
•�������� 恰当选择船型参数(esp.主尺度)
•�������� 减少附体
– NOTE:
•�������� 若改变湿表面积致使船体形状改变过多,则会引起其 他阻力成分的变化,有时得不偿失!
•�������� 1) 使湿表面积减少( S↓ )
•�������� 2) 减小船体表面粗糙度Roughness(DCf↓)
•�������� 方法:使表面尽可能光滑
•�������� BUT:办法不多,效果不大
3.2 现代方法与新思路
•�������� 1) 降低密度(ρ ↓)
•�������� 方法① :将船体抬出水面, ρair<< ρwater
•�������� NOTE:
•�������� 经济性不能与普通的排水型船相比
抬出水面付出代价,仅适用于小艇
– 方法②:气膜(泡)减阻 Air lubrication
•�������� 使紧贴船体表面由一层空气薄膜或水汽混合物覆盖
•�������� NOTE:
– 微气孔容易塞结
– 气泡易逃逸
•�������� ) 降阻剂
– 方法:船体表面不断喷注稀释后的高分子聚合物 溶液
– 机理:抑制湍流加剧,降低湍流程度,减小阻力
– 效果:平板减阻60%~70%,船模减阻30%
– NOTE:实船难以应用!
•�������� 聚合物相对分子质量及其分布有讲究
•�������� 成本高
环保性差
•�������� 3) 控制边界层以降低摩擦阻力系数( Cf ↓ )
– 方法①:边界层抽吸,使得边界层的层流区延长
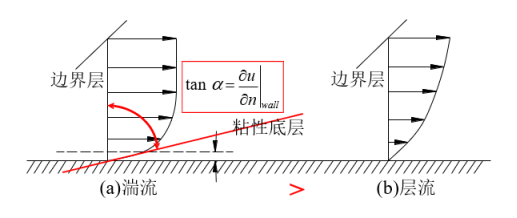
•�������� 控制边界层以降低摩擦阻力系数( Cf ↓ )
– 方法② :自物体表面沿着流动方向向后吹喷流体,使得湍流边界层变厚,界层速度梯度↓
•�������� 3) 控制边界层以降低摩擦阻力系数( Cf ↓ )
– 方法② :自物体表面沿着流动方向向后吹喷流体,使得湍流边界层变厚,界层速度梯度↓

•�������� 4) 仿生材料
– 表面波纹(鲨鱼表皮)
– 弹性覆盖层(海豚表皮)
– 疏水表面减阻(荷叶)
第4节 粘压的成因及特性
4.1 船体粘压阻力产生的原因
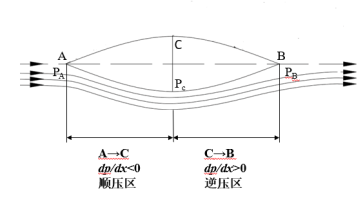 •�������� 1)无界域理想流体
•�������� 1)无界域理想流体
•�������� 前驻点A:
VA=0; PA=Pmax
•�������� 最大剖面点C:
Vc=Vmax; PA=Pmin
•�������� 后驻点B:
VB=0; PB=Pmax
•�������� 理想流体力学理论导致达朗贝尔谬论→No Drag
2) 实际粘性流体
 ① 有边界层分离时的Rvp
① 有边界层分离时的Rvp
② A→C:V↑ P↓
③ C→B:V↓ P↑
④ 分离点D: V=0
⑤ DD’以下:回流→界层分离→P后体↓→首尾压差(Rvp)
⑥ 能量观点:尾部不断产生的脱体旋涡耗损能量→Rvp
⑦ 分离点前移→界层分离区↑→Rvp↑
 实际粘性流体
实际粘性流体
① 无边界层分离时的Rvp
② Rvp不分离< Rvp分离
4.2 粘压阻力特性(影响因素)
•�������� 最重要的是物体后端的形状:收缩要缓和
– 粘性作用和物体后部的纵向的逆压梯度是粘压阻力产生的原因。
– 后体收缩缓和→沿流向速度变化↓→纵向压力梯度↓→减少分离乃至避免分离→Rvp↓
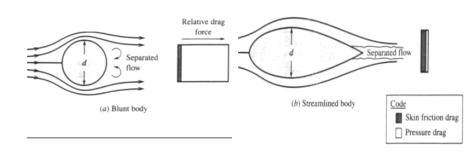
•�������� 前体形状:避免肩部
– 前体过于肥短,形成肩部→前体流线过快扩张→ 最大剖面处速度很高,压力很低→后体急剧减速,逆压梯度↑→分离点前移,分离更严重→ Rvp ↑
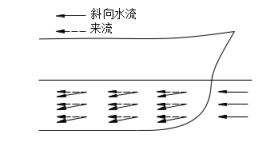 – 船体舭涡
– 船体舭涡
•�������� 低压,埋首
球鼻艏
•�������� 边界层的流动状态
– 边界层发生分离时,与分离区域的大小有关
•�������� 层流界层更易分离, Rvp层流
•�������� Cvp~f (Re)
– Re<2×105,层流, Rvp较大
– 2×105<Re<3.5×105,过渡流,Rvp急降
– Re>3.5×105,湍流, Cvp近似常数
•�������� 若Res,Rem>Recr,Cvps=Cvpm
– 边界层不发生分离时,Re↑→Rvp↓
4.3 降低粘压阻力对船型的要求
•�������� 基本思想:避免分离,如不能避免分离,则尽可能减小分离。
•�������� 注意后体形状
– 去流段足够长度
– 后体形状收缩要缓和
•�������� 船型变化不宜过急
•�������� 低速肥大船,可采用球鼻艏
4.4 船体粘压阻力处理办法
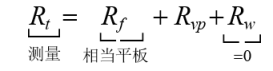 •�������� 深水叠模试验(Rigid surface)
•�������� 深水叠模试验(Rigid surface)
•�������� 船模试验(Free surface)
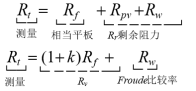 Froude换算法(二因次法)
Froude换算法(二因次法)
三因次法
5. 确定粘性阻力的方法
5.1 确定粘性阻力的尾流测量法
•�������� 毕托管测量方法
•�������� LDV(Laser Doppler Velocimetry)
•�������� PIV (Particle Image Velocimetry)
•�������� etc.
•�������� 毕托管测量方法
•�������� 假定:
•�������� 船后尾流平面内的动量损失完全由粘性所致;
•�������� 船模近后方平面和充分远处平面之间无能量损失;
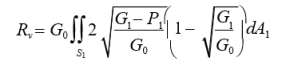 •�������� 不计波浪影响。
•�������� 不计波浪影响。
– 具体做法:
在船后(约1/2船长处)测量平面S1处(相对船模固定)某一深度上横向布置一组毕托管(随船模前进), 测得S1截面处各点的相对总压力G1和相对静压力P1。 同一速度下,改变毕托管深度,反复测量,即可求出 该平面各点G1和P1,积分后即可求出Rv。
5.2 船舶粘性阻力理论计算概述
•�������� 边界层理论概述
– 船体边界层特点:
•�������� 前2/3薄边界层,薄边界层理论适用
•�������� 后1/3边界层变厚甚至发生分离,薄边界层不再适用
NS(RANS)方程
•�������� NS方程理论概述
– N-S方程 (DNS)
– RANS方程(湍流)
– DES/LES (湍流)
•�������� NS方程理论概述
– RANS方程(湍流)
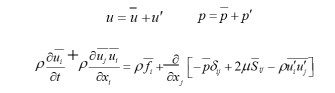
•�������� 上述方程不封闭,需要借助湍流模型。湍流模型的选 择和处理需要考虑近壁面流动特性。
•��������
第9章 兴波阻力
一.船行波的形成和凯尔文波系
兴波阻力Rw是船舶航行过程中兴起波浪的能量代价。
船舶兴起的波浪:船行波、破波
船行波:留在船后并不断向外传播(又称:自由波)。
破波:兴起后很快就破碎的波浪,通过粘性耗散消失(丰满船,Cb =0.78以上)。
平面进行波特性
任何一种复杂波系,均可视为由简单的平面进行波(或称:基元波)组成。
z = Acos(kx - wt)
A : 波幅 波高 H=2A
k : 波数 波长λ=2π/ k
ω: 波频率 波浪周期 T =2π/ω
1) 波速:波形传播速度(波动的“相速度”)
2) 波能:一个波长的总能量 ![]() ,对于波长为λ,波宽为b的波面的波能
,对于波长为λ,波宽为b的波面的波能![]()
3)波能传播速度
由于水质点以一定的半径作规圆运动,其动能不变,但位能却发生变化,以致波能沿波形传播方向转移,由于位能是总能量的一半。
4)船行自由波
如假定为线性问题,船体波系可以看作基元波的叠加。
θ向的平面波,波形为![]() = Re{A(q )e- ik ( x cosq + y sinq ) } 。
= Re{A(q )e- ik ( x cosq + y sinq ) } 。
将所有可能的传播方向的基元波(单色波!)叠加,即得整个船行波的波系。
- 船行波的形成
船行波的形成是由于水流流经船体弯曲表面时,沿船体表面压力分布发生变化,导致船体周围水面上升或者下降,在重 力和惯性力的作用下形成船波。
船行波的形成与压力、液面的高度等相关,沿船体水线及远前方液面可应用伯努利方程:
F点:V, P0 , z=0
A点: ![]()
B点: ![]()
C点: ![]()
![]() ,
, ![]()
波高 ![]()
�������� 船行波的实际情况
实际水面抬高小于ZA = 2g ;
由于惯性作用,最高水面位置存在滞后现象;首波峰总出现在首柱稍后位置,尾柱稍前为波谷。
扰动 离开平衡位置 重力和惯性力 绕平衡位置震荡 形成波浪
2. Kelvin波系与船行波的组成
1)压力点的兴波图形
Kelvin波:压力点在水面下作匀速直线运动时的兴波波形图。
2) 船行波的兴波图形
船周围的压力场→多个运动压力点,但首尾两端压力变化最大→用两个压力点的兴波近似描绘船体兴波。
3) 船行波的特征
① 随船移动的波系比较明显的是首尾两个波系,各由横波和散波组成。
② 船波系集中与Kelvin角所限的扇形区内。
③ 首横波第一峰始于船首柱略后,尾波系自尾柱略前始于波谷。
④ 波系的各散波之间,散波与横波之间互不干扰。
⑤ 首、尾横波系在船尾混合、干扰,形成合成横波。
二. 船的首尾波系及其干扰
- 首尾横波的干扰
1)兴波干扰
实际船体存在船首波系和船尾波系,两波系中的横波在船尾 处相遇而叠加,这种现象称为兴波干扰。
2) 兴波干扰结果
有利干扰
船首横波波峰和船尾横波波谷相叠→合成波波幅减小,兴波阻力减小。
不利干扰:
船首横波波谷和船尾横波波谷相叠→合成波波幅增大,兴波阻力增大。
3)影响干扰结果的因素
首尾两横波的相对位置
�������� 兴波长度mL:船首横波的第一个波峰和船尾横波第一个波峰之间的距离。
首尾横波的干扰情况由mL和波长决定。
a) 兴波干扰的三种情况 :
1)q=0, 两横波相位差为0,峰峰叠加,不利干扰
2)q=0.5, 两波相位差为π,峰谷叠加,有利干扰
3)q任意, 两波相位差为2πq,一般干扰
b) 船长L:L变化,mL/λ变化,从而兴波干扰结果发生变化
① 平行中体变化,有间距均匀的阻力峰点出现;
② V 越高,剩余阻力波动越大;
③ 剩余阻力的波动随着船长的增加而减小。
c) 菱形系数Cp
Cp对两横波的干扰作用有较大的影响。
① Cp小,两端瘦削 → 水压力小 → mL小;
② Cp大,两端较钝→ 水压力大 → mL大。
- 傅汝德圆圈(P)理论
1) P理论预测兴波干扰
大量的试验资料分析表明:不同形状的船舶在不同速度下,虽然兴波长度不同,但自船首横波第一个波节点至尾横波第一个波谷之间的距离均可以表示为CpL。

•�������� 当q=0.5时,有利干扰:Cp L / l = n - 1/ 4
•�������� 当q=0时,不利干扰:C p L / l = n - 3 / 4
•�������� 定义ⓟ��������为船速V与波长为CpL的波速之比
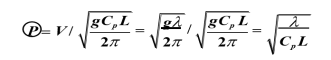
波阻峰点:
波阻谷点:
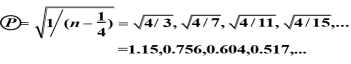
三. 兴波阻力的特征
- 兴波阻力的成因
1) 压力的观点
![]() 首横波在艏柱稍后以波峰开始 首波面>尾波面>船首压力>船尾压力
首横波在艏柱稍后以波峰开始 首波面>尾波面>船首压力>船尾压力
尾横波在艉柱稍前以波谷开始 >首尾压差(兴波阻力)
2) 能量的观点
产生波浪需要能量(由船提供)>体现为船的兴波阻力
- 兴波阻力与波浪参数的关系
1) 波速C=航速V
2) Rw∝bH2
Vg = 1/2C
- 兴波阻力一般特性
1) 兴波阻力的一般规律
根据傅汝德定律,对给定船型,有Cw=f(Fr)
2) 兴波阻力的组成

自然兴波阻力:首尾波系中未受干扰的横波以及两波系的散波所产生的兴波阻力;
兴波干扰阻力:首尾横波干扰后的兴波阻力。
3) 兴波阻力曲线形状
在一定Froude数范围内,兴波阻力曲线出现峰、谷交替的现象。
根本原因:首尾横波干扰
兴波干扰结果取决于船首尾横 波 的 相 对 位 置 mL/ λ V↑,λ↑,相位发生变化有利、不利干扰交替出现 Rw曲线出现峰谷交替现象。
- 兴波阻力与船型的关系
1) 不同船型的兴波阻力:
Fr<0.15,Cw均很小,
同Fr条件下,丰满船>瘦削船。
Fr≈0.5,存在峰值。
2) 船型对兴波阻力的影响
兴波阻力中的“自然兴波阻力”受船体形状(主要是首尾端形状),特别是首部形状的影响很大;
同Fr下,丰满船的Cw比瘦削船的大;
受干扰阻力的大小取决于mL/λ , mL与船型、速度有关, λ与船速有关;
兴波干扰主要与L和Cp有关。
有利船长;不利船长
四. 确定兴波阻力的理论计算方法
1) 基本假定
水是无粘不可压缩理想流体;
流动无旋有势,满足基本方程:Laplace方程;
微幅波假定:波高相对波长为小量。
2) 基本思路
船舶运动速度V = (V , 0, 0)
取随船的运动坐标系 流动为定常,则速度势 ![]() =
= ![]() -V0 x,
-V0 x,
即总速度势可分解为船舶产生的扰动势与恒定的来流势。
速度势![]() 是Laplace方程的解,为使
是Laplace方程的解,为使![]() 是唯一确定的解,则需满足下列边界条件:
是唯一确定的解,则需满足下列边界条件:
自由液面运动学边界条件:![]() ;
;
辐射条件:远前方无波的条件。
圆柱绕流=均匀流+偶极子 思路:奇点置换物体。
船体兴波阻力的求解:
通过在船体上布置源汇,使源汇产生的速度势满足兴波求解的控制方程和边界条件,从而求解速度势。
3) 几种线性理论方法简介
1) 薄船理论
将自由表面边界条件简化为在静水面上满足,船体表面上分布 奇点简化在船体纵中剖面上满足,这种理论称为薄船理论,以 Michell积分为代表。
2) 细长船理论
若引入船舶宽长比及吃水长度比均为小值,自由液面边界条件 简化为在水平面上满足,船体表面奇点简化在船体中纵轴分布, 相应的兴波阻力理论称为细长船理论,以Noblesse细长船理论 为代表。
3) 扁船理论
若引入船舶吃水宽度比和吃水长度比均为小值,自由液面边界 条件简化在水平面上满足,船体表面分布奇点简化在船体设计 水线面上满足,相应的兴波阻力理论称为扁船理论。该理论适 合于浅吃水的扁船。
4) 密契尔公式
适用范围:“薄船”, B<<L .
奇点(源汇)分布在船的中纵剖面上。 兴波阻力计算公式:
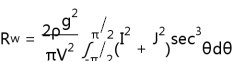
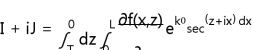
表征船体表面形状的函数 y = ± f ( x, z)
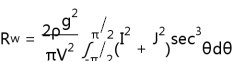
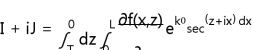
影响![]() 的主要是水线的纵向梯度:
的主要是水线的纵向梯度: ![]() ;
;
z < 0,近水面处的线型对兴波阻力影响大,离水面深处的线型影响小;
k0 = g /V2 船速越低,线型的影响范围越向水面处集中。
五 确定兴波阻力的试验方法
- 船模试验方法
1) 叠模试验法
Cwm = Ctm-Cvm
2) 二因次法
�������� Crm = Ctm-Cfm
3) 三因次法
Cwm = Ctm-(1 + k)Cfm
- 波型分析
1) 基本原理
局部波系
在船体加速过程中形成的波系,当航速恒定后, 它随 船一起前行但不向外传播,因此它对匀速直线运动船 舶不形成阻力;
自由波系
在船前进时不断向船后扩散的波,需要船体不断向其 提供能量以维持其稳定的波系。
2) 自由波系表达式
![]()
![]()
波型阻力
![]()
将Rw和船后自由波系的波幅函数联系起来。
3) 波型分析的实质及特点
波型分析的实质
波型分析的实质是利用测量所得的波形要素推算波幅函数,进而利用波幅函数计算兴波阻力。
波型分析的特点
避开了船体型值和尺度,直接从船舶航行时产生的物理现象(兴波)的实际数量出发。
4) 波型分析的基本思路
测量贯穿船后整个自由波系的某些断面的波型信息(波高或者波斜率等)>傅里叶变换(Fourier)和逆变换>得到波幅函数C(![]() )和S(
)和S(![]() )> Rw
)> Rw
5) 方法类型
纵切法
在船模的一侧与船中纵剖面平行的方向上取一条或者更多的纵向截面,测量波型参数。
优点:装置简单,记录方便。
缺点:受池壁干扰,需在反射干扰前截断,因此存在截断误差。
N-S 法:采用一种渐近波形曲线对截断点后的波形做理论延拓和拟合
影响纵切法波形测量精度的因素:
�������� 波形截取长度
�������� 纵切线距船模之距离
�������� 船模预行段长度
横切法
在船后L/2~L取横向截面测量波型参数。
优点:不受池壁干扰。
缺点:测量技术复杂,测量精度受轨道高低不平及船后伴流等多种因素的影响。
六.减小兴波阻力的方法
1.减小常规船兴波阻力的方法
兴波阻力特性:
兴波阻力是Fr的函数;兴波阻力与波高的平方成正比;一定Fr下,兴波阻力曲线呈现峰谷交替的现象; 兴波干扰结果与船型密切相关。
基本思想:减小兴波幅值
1)经典方法
①选择恰当的主尺度和船型参数L/B,Cp,Le,进水角等,应用ⓟ��������理论根据给定航速,合理选择L和Cp避免处于波阻峰点。
②设计良好的首尾形状(横剖面面积曲线 )
2)造成有利的波系干扰
常见的为采用球鼻船首。
机理:适当大小和位置的球鼻→球首波系与主船体波系形成有利干扰→合成波波高减小→Rw减小。
3)消波水翼
适用对象:高速船/艇
机理:适当位置、深度的水翼,形成波穴(低压区),可使船首波减小,兴波阻力减小。

4)压浪板、压浪条
压浪板:增加船长,改善尾倾 压浪条:压制首部兴波。
2.应用不同设计概念减小兴波阻力
1)双体和多体船设计概念
双体船:与同∆��������的单体船比,单个片体的L/B大,Rw↓
多体船: L/B大,且可利用前后体形成兴波有利干扰,Rw↓
2)使船体抬出水面设计概念
将船体抬至水面滑行或使船体离开水面来减小Rw, 有滑 行艇,水翼艇,气垫船等。
3)船体下潜设计概念
使船体排水体积部分或全部移向水面以下,减小兴波,减 小Rw。
4)复合设计概念
七.破波阻力
- 破波阻力的成因
破波阻力的发现:
对于较丰满船型 Ctm - (1+ k)Cf > Cwm
且二者差值随Fr增大而增大:
Ctm = (1+ k)Cf + Cwp + Cwb
- 破波阻力的测定
- 破波阻力的特性
① 是由于自由面引起的;
② 丰满船型高速航行情况下,Rwb不可忽略;
③ 几何相似丰满船型,Rwb随着Fr增加而增加;
④ 服从Froude比较率;
⑤ 压载比满载时Rwb要大
影响因素与减阻措施:
1 与B/T,Le有关-----B/T↓Le↑
2 采用球鼻艏船型能减少Rwb
七.阻力分类的补充说明
1.阻力分类的再认识
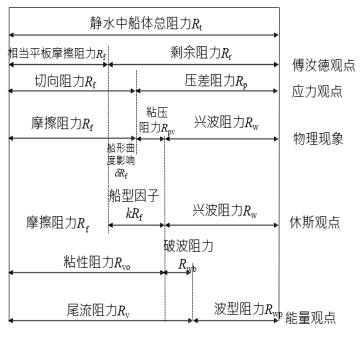
第十章 附加阻力
一.附体阻力Rap
- 成因
– Rap为船体之外的附属部分受到的水阻力。
- 特点
主要成分为 阻力
较短附体主要成分为 阻力
较长沿流线方向安装的附体主要成分为 阻力
- 确定方法
由资料或经验公式估算:
模型试验:带附体船模试验总阻力Rm+DRm和裸 船体船模试验总阻力Rm之差来确定。
- 减小措施
附体沿船体流线方向设置→ Rvp↓
减少附体湿面积→ Rf↓
附体沿流向具有流线型对称剖面 →Rvp↓
二.空气阻力Raa
- 成因
Raa为船体水线以上部分和上层建筑所受到的空 气阻力。
- 特点
– 主要成分为 阻力
– 风速大小、方向和船体外形
- 确定方法
– 粗略估算:![]()
– 经验公式:![]()
- 减小措施
上层建筑尽可能低而长,尽可能减少迎风面积At
上层建筑前段流线型,后段阶梯形。
三.波浪中的阻力增值Raw
- 成因
– 船舶在风浪中航行时的阻力将较静水时大,所增 加的阻力称为波浪中船舶的阻力增值(Raw)。
– 引起波浪中阻力增值的原因:
(1)船体运动
纵摇 升沉 横摇 首摇 + 纵荡 横荡
这一部分与摇摆运动相关的阻力增值可记为Rawʻ�������,与摇摆参数相关 (e.g. amplitude, velocity, acceleration, phase, frequency, etc.)
– 引起波浪中阻力增值的原因:
(2)船体对波浪的绕射作用(波绕过障碍物而传播的现象)
船体表面不可穿透→反射水波→能量损失
波浪作用→压力场产生周期性变化→平均值较静水阻力↑
淹湿性→浸湿面积S↑
这一部分与绕射效应相关的阻力增值可记为Raw ”,与波浪参数相关 (e.g. wave length, height, etc.)以及入射角相关
- 特点
Raw与风浪的大小、方向,船型、航速等因素有关
(1)波浪因素
Raw与波高平方成正比;
Raw主要取决于纵摇pitch及垂荡heave的强度,以及船体运动和 波浪的相位关系;
尤其注意要避免纵摇周期与波浪周期相近;
λ / L≈1.0时,纵摇谐振区,Raw峰值。
(2)船型因素
静水中阻力较低船型其Raw较低;
V 型首Raw < U型首Raw (耐波性);
Raw满载< Raw压载(运动幅度);
相同波高,Cb ↑,波浪增阻↑。
- 减小措施
方形系数:控制Cb,不能太大。
航区:海况良好的航速Raw较小。
船首剖面:V 型首Raw小。
装载情况:满载时运动幅值小,Raw小。
- 确定方法
1) 失速:
由于风浪中的阻力增值,如保持静水中的功率,航速 必然下降。这种航速的减小称为速度损失,即为“失 速”。
2) 储备功率:
由于风浪中的阻力增值,如维持与静水条件下相同的 航速,则需较静水功率为大的功率。增加部分称为“ 储备功率”。
航区海况、气象条件、操纵性等问题。
第十一章 船模实验
一.船模阻力试验的目的、试验设备概述
1. 船模阻力试验的目的
主要研究船模在水中等速直线运动时所受到 的作用力及其航行状态。
2. 船池及其设备
最重要的是拖曳水池:Towing Tank
– 水池类型
1) 重力式:
等阻力法。
借砝码的重力拖动船模,测出船模匀速时的速度,改变砝码 的质量,可得到船模阻力和速度的关系曲线。
2) 拖曳式(近代):
等速度法。
速度精度高( 1/1000 ) ,设备要求高(轨道平直,高度差 不超过1s)
3) 水池设计考虑因素
长度:试验速度、船模大小
宽度:船模大小,池壁对试验的影响(>2Lm)
深度:浅水效应,池底对试验的影响(>Lm)
4) 长沙理工大学拖曳船池简介
– 船池尺度:60×1.5×1.8
– 设计拖速:0.05m/s~2m/s
5) 拖曳水池试验类型小结
a)阻力试验Resistance test
b)自航试验Self-propulsion test
c)螺旋桨敞水试验open water propeller test
d)稳性试验、耐波性试验、操纵性实验
e)海洋工程试验
3. 阻力试验的依据
1) 实现全相似的条件
2) 船模试验只能在部分相似条件下进行
a) 仅Re相似条件也难以满足。
b) 实际上船模试验仅在满足Fr相似条件下进行。
c) 试验中对于粘性力相似问题的考虑:
- 对船模采用“激流”措施
- 表面粗糙激流法;激流杆法;激流丝法(最普遍)
- 粘压阻力进入“自模区”(Cvp ≈const)
- 船模试验的雷诺数必须在2×106以上。
4. 阻力试验的方法
1) 试验准备
制作模型
激流: Laminar flow ~ Turbulent flow
称重(排水量)
安装(对称、平衡、不受约束)
2) 测量数据
速度:拖车速度(稳定均匀)
船模阻力:与速度同时记录(电测阻力仪)
纵倾角、升沉等
3) 影响因素
池壁影响、消波
拖车速度(加速度、平稳度)
轨道平直度
人为干扰,测量仪器精密度
尺度效应
二. Froude换算法(二因次换算法)
- 基本思想
- Rt (Fr, Re) = Rf (Re) + Rr (Fr)
- 相当平板假定:
Rf =“相当平板”的Rf
- 兴波阻力Rw与粘压阻力Rvp合并为剩余阻力
Rr,且适用于Froude比较定律:
![]()
![]()
- 换算关系
- 局限性
1) 粘性力与重力引起的现象互不干扰
2) 将粘压阻力Rvp并入剩余阻力,使之服从比较律
3) 用相当平板代替三维船体表面
大部分情况下工程上可用
a) 粘压与重力相互影响较小,工程上可以忽略不计
b) Cr(Fr) =Cw+Cvp+ δCf中Cw为主
c) ΔCf 可起到一定的调节作用
该方法简单实用。
•�������� 注意:随着L↑丰满度↑,Froude换算法不再 适用
– L↑ →λl ↑→尺度效应更加明显→选用小尺度模型 进行试验,将会产生较大的误差
•�������� 采用过小模型,将过量估计实船阻力
阻力预报偏大(有效功率Pe偏大)R↑→ Pe↑
航速预报偏低R↑→ Vs↓
粗糙度补贴系数为零或者负值
能满足实际工程需求,但尚有欠妥之处
三.三因次换算法(1+k法)
- 基本思想
Ct = Cw (Fr ) + Cv (Re)
兴波阻力Rw与Fr相关,相应速度下Cwm = Cws
认为Cvp与Cf 之比是一常数k,为形状系数;(1+k)为形状因子,仅与船体相关:
Cvp = kCf;Cv =(1+ k )Cf
- 换算关系
- 局限性
形状因子(1+k)多借助低速试验方法确定(减少兴波影响),但低速试验层流影响大,使得结果不可靠。存在由Re无法相似带来的尺度效应问题,没有计及粘性与兴波相互干扰问题。
四. 几何相似船模组试验
- Telfer几何相似船模组试验
几何相似船模组是指几何相似而大小不等的 一系列船模的统称。
1) 用途:
a) 验证阻力换算方法的准确性
b) 比较不同换算方法的合理性
c) 研究形状因子及推进效率中各成分的尺度作用等
Telfer用24000t油轮的几何相似船模组进行系 列试验,试验结果表达成Ct随Fr及Re变化的曲线图。
2) 基本思想:
①以总阻力系数Ct为纵坐标,Re为横坐标
②对于每一给定尺度之船模,将其总阻力系数Ct随Re变化关系绘制成曲线
③按照图谱趋势外插至实船雷诺数Res,其纵坐标即代表光滑实船总阻力系数。
- 验证Froude换算方法
关于假定一:粘性和重力引起的现象互不干扰
Ct (Fr, Re) = Cf (Re) + Cr (Fr)
– 互不干扰假定成立→Fr等值线? 相互平行
– 实际上:等值线间距并不完全平行,甚至有波动
– BUT:总体趋势大致平行,上述假定基本正确
- 三因次方法验证
三因次换算结果 小于 Froude换算结果
- 比较不同换算方法的合理性
1) 由Froude换算得到的实船总阻力系数随船模 尺度的增加而有较明显降低。
2) 采用三因次换算法可以大大减少这种尺度作 用,较二因次法更为合理。
3) 三因次换算法存在问题:
1+k=cons
小尺度模型船,会引起(1+k)↑
�������� 采用Froude换算方法,将过高估算实船阻力;所得Cts随船模尺度的增加而有较明显降低
�������� 采用三因次换算法可以大大减小尺度作用,较Froude换算法更为合理。
第十二章 船型对阻力的影响
一.船型对阻力影响的基本概念
- 船舶阻力数据的表达
1) 数据表达的目的
比较船型阻力性能的优劣(船型不同,大小相同或相近 的船舶)。
2) 阻力数据表达法
船舶阻力随V不同而不同,只能在“相同速度”下比较。 相同速度下,不同船型的船舶阻力还受尺度大小的影响。 应将两船型各按几何相似变换,化为“同一尺度”,
然后在“同一相对速度”下比较。
�������� 在船舶设计过程中,比较不同船型的优劣时,应首先把不同 船型的阻力资料换算到大小相同的船舶之阻力,然后在相同 速度时比较单位排水量总阻力Rt/Δ的大小作为判断不同船型 阻力性能优劣的衡量标准。
- 船型、航速与阻力性能的关系
1) 船型
(阻力学科上)指船体水下部分几何形状。
2) 船型参数
船体形状:横剖面面积曲线形状;满载水线面形状;首尾形状
3) 船型影响与航速密切相关
不同速度区间内船型参数对阻力的影响有所不同(程度, 性质)
阻力优良船型:在某一速度范围内阻力较低的船型
4) 两类船型变化方式
① 仿射变化
�������� 仿射变化的概念
变化前后,船体表面各对应坐标各按同一比例放大或缩小。
x1=mx;y1=ny;z1=pz
�������� 仿射变化的特点
•�������� 主尺度成比例变化
L1=mL; B1=nB; T1=pT
•�������� 线型特征不变(无因次坐标方程不变)
•�������� 无因次船型系数之数值在船型仿射变换后不改变
•�������� m=n=p:几何相似
•�������� m*n*p=1:排水体积不变
两类船型变化方式
① 仿射变化
② 改变线型特征
改变了各种丰满度系数Cb,Cm,Cp。
实用上采用其变化对阻力影响最大的因素来表达船型变化。
e.g. 排水体积纵向分布情况,线型及首尾形状。
5) 不能仅从阻力观点片面地评判船型优劣或者选择船型参数
�������� 阻力大小并非决定船型优劣的唯一因素,有时并非重要因素;
�������� 仅从性能考虑,操纵性、稳性、耐波性等对船型的要求可能与阻力要求相互矛盾。
二 .船体主尺度的影响
- 几何相似船舶∆��������对Rt 的影响
1)Fr相等时,∆��������大小的影响
2) V 相等时,∆��������大小的影响:
相当于在指定航速下选择船舶大小的问题。
V 相等, Rt /∆��������随船长增加而减小。
- 排水量长度系数对阻力的影响
1)排水量长度系数∆�������� /(0.01L)3 :代表了船舶的瘦长程度。
�������� ∆�������� /(0.01L)3大,意味着同样长度范围分布更多Δ,肥短;
�������� ∆�������� /(0.01L)3小,表示船型瘦长。
2)排水量长度系数变化有两种情况产生
�������� Δ一定,保持Cm,Cp和B/T不变,同时变化B和T,使L相应变化;
�������� L一定,保持Cm,Cp和B/T不变,同时变化B和T,使Δ相应变化;
2.2 L变化,讨论∆�������� /(0.01L)3对阻力的影响
1)对摩擦阻力的影响
2)对剩余阻力的影响
3)对总阻力的影响
4)船长选择
- 总布置
- 船舶性能(阻力,操纵)
- 对民船涉及经济性
原则: L一般取略小于Lopt ,阻力增加不多,造价可望下降。
∆��������变化,讨论∆�������� /(0.01L)3的影响
1)对摩擦阻力的影响
L一定,∆��������↑→Rf /∆��������↓。
2)对剩余阻力的影响
3)对总阻力的影响
∆��������对Rt /∆��������的影响取决于Rf /∆��������和Rr /∆��������所占比例。
① 对大Cp船(低速船)
∆��������↑(Rf /∆��������↓, Rr /∆��������→), Rt /∆��������有所下降
② 对小Cp船(高速船)
∆��������↑ (Rr /∆��������急剧增加),Rt /∆��������↑
∆�������� /(0.01L)3对阻力的影响
1) 基本规律
�������� ∆��������一定,L↑( ∆�������� /(0.01L)3 ↓ ),Rf ↑,Rr↓;
�������� L一定,∆�������� ↑ ( ∆�������� /(0.01L)3 ↑ ),Rf /∆��������↓,Rr /∆��������↑;
�������� ∆�������� /(0.01L)3↑,Rf /∆��������↓,Rr /∆��������↑。
2) 不同船舶的∆�������� /(0.01L)3选取原则
�������� 低、中速船宜取大(肥而短);
�������� 高速船宜取小(瘦而长);
�������� 由于∆�������� /(0.01L)3的变化对Rf 、Rr 影响相反,对于给定的V 存在对应于Rtmin的最佳 ∆�������� /(0.01L)3 。
∆�������� /(0.01L)3对阻力的影响
1) 基本规律
�������� ∆��������一定,L↑( ∆�������� /(0.01L)3 ↓ ),Rf ↑,Rr↓;
�������� L一定,∆�������� ↑ ( ∆�������� /(0.01L)3 ↑ ),Rf /∆��������↓,Rr /∆��������↑;
�������� ∆�������� /(0.01L)3↑,Rf /∆��������↓,Rr /∆��������↑。
2) 不同船舶的∆�������� /(0.01L)3选取原则
�������� 低、中速船宜取大(肥而短);
�������� 高速船宜取小(瘦而长);
�������� 由于∆�������� /(0.01L)3的变化对Rf 、Rr 影响相反,对于给定的
V 存在对应于Rtmin的最佳 ∆�������� /(0.01L)3 。
- 宽度吃水比的影响
1) B/T对Rf 的影响
B/T对Rf 的影响通过对湿面积S 的影响体现,试验资料表明S与B/T有关,但影响不大。
2) B/T对Rr的影响
B,T的分别影响:B增大,散波增大、T增大,横波增大。
综合来说,B/T增大,Cr有所增大,但在某些速度段可能相反。
3) B/T对总阻力Rt的影响
一般认为:
�������� B/T增大时,Rt / D 略有增大
�������� B/T对 Rt / D的影响不大
B/T的实际选择主要不是基于阻力观点:
�������� B的选择——布置,稳性出发
�������� T的选择——港口、航道情况
�������� 由B/T与L的关系而定
目前倾向于:对中低速船略为增大B值,使L/B ↓, Cb ↓
三.方形系数和中横剖面系数的影响
- 方形系数的影响
方形系数对阻力的影响
Cb的影响与船速有关, 因为Cb对兴波阻力影响敏感。
Cb对摩擦阻力影响较少,对剩余阻力影响R t /Δ较大
总体: Cb增大,Rt /△增大,而且从某一Cb值开始, Rt /△的增加将更快,此Cb值称为该Fr时的临界方形系数Cbc。
Cb的选取
1 .由经验公式确定临界方形系数
Cbc = 1.05 - 1.68Fr(服务航速)
= 1.08-1.68Fr (试航航速)
2 .由Cp 、Cm与Cb 的关系确定(参见p275图6-15)
· 民船从经济性考虑,在不显著增加(Rt /∆��������)的前提下,取较大的Cb
Cm 对阻力性能影响较小。
- 中横剖面系数的影响
Cm 值的选取
中低速船: Cm 偏大为好。(Cb给定时可使Cp↓→Rw↓)
高速船: ∵ Cb小,∴ Cm 主要考虑线型的光顺
Cm 的选取实际上取决于Cb
四. 横剖面面积曲线形状的影响
- 棱形系数的影响
表征船舶的排水体积沿船长的分布情况。
∆��������一定,L一定时:
---Cp大,表示排水体积沿纵向分布比较均匀,首尾较丰满;
---Cp小,表示排水体积比较集中于船体中部,首尾较瘦削。
讨论棱形系数对阻力的影响
① 对Rf 的影响:
当Δ、L不变时,Cp 变化对S 影响很小→对Rf 基本无影响。
② 对Rr :Cp对Rr影响很大。
当Fr<0.2
Cp小则Rr 小,但影响甚微; 当0.2<Fr<0.3
Cp小则Rr 小,影响显著; 当Fr>0.3
适当大的Cp反使 Rr ↓。Fr一定,存在对应(Rr /Δ)最小的Cpopt。
Cp对Rr影响的物理解释
Cp对Rr的影响主要与不同航速时的兴波情况有关;
波峰与首垂线的距离:![]() =0.372
=0.372![]()
Cp对Rr影响的物理解释
�������� 低速时, Rw 极小, Cp的影响小;
�������� 中速时,首尾尖瘦,对Rw有利。
中速时,高压区仅在首部不太大的范围, Cp小,使高 压区的水压力在运动方向上投影减小,从而Rr ↓;
Cp对Rr 影响的物理解释
�������� 高速时,Fr↑,V↑ → 首波峰后移;
Fr↑,V↑ → λ ↑,首部波浪高压区范围↑。
(低速时,波浪高压区占0~15%L;Fr=0.3时,占25%L。)
Cp对Rr 影响的物理解释
�������� 高速时,大的Cp使排水体积在高压区较均布,减小高 压区在运动方向上的投影将使得Rw ↓。
最佳棱形系数曲线
实际民用船舶设计中,主要从船舶的使用性和经济性出发。
Fr<0.3的普通民船的Cp选取原则在不显著增大( Rr /Δ)的前提下,尽可能选较大Cp 。
- 浮心纵向位置的影响
浮心纵向位置即As (x)的形心的纵向位置,记为xc。
xc反映排水体积对船中分布的不对称程度。
一般以占Lbp的百分数表示: xc = xc / Lbp
xc > 0 表示浮心在船中之前,首肥尾瘦。
xc < 0 表示浮心在船中之后,首瘦尾肥。
不同船型xc 的选择
☆基本思想
不同速度范围的船型Cw 和Cpv所占比重不同,对xc 的要求各异。
◇低速船: Rw 所占比重小,注意减小Rpv →应在中前。
◇高速船: Rw 所占比重大,注意减小Rw →应在中后。
◇中速船:适当移向船中。
☆ xc 选择原则
“高速宜后,低速宜前”
- 平行中体长度和位置的影响
中低速船船体长度大致分为:进流段Le,平行中体Lp,去流段Lr
平行中体指As(x)=Am 的一段,即基本上与船中横剖面形状相 同的一段。
① 简化工艺,降低造价
② 增加舱容
1)Lp对阻力的影响
L、∆��������、Cp一定时,Lp↑→两端尖瘦→中低速下Rw↓且 利于建造及舱容使用。
若Lp过大或过于偏前、偏后,则易形成“肩波系”, 产生涡流→Rvp↑
高速船不宜采用Lp(一般认为Fr >0.24即不应采用)
2)Lp及其位置的确定
- 横剖面面积曲线两端形状的影响
1) 主要形状
a) 凹形
b) 微凹
C)直线形
2) 一般原则
① 首端取决于兴波的比重和首波峰位置(参见Cp 的讨论)。
② 尾端取决于粘压阻力,后端影响较前端小,一般取直线
③ 不同航速船舶的横剖面面积曲线两端的形状可概括为: 低速船:两端宜为直线形;
中速船:前端宜取微凹或凹形,后端直线或微凹;
高速船:两端宜取直线或微凸。
五.满载水线形状的影响
- 满载水线面积系数
常用水线面系数Cwp表示。
(Cwp与稳性,适航性和快速性有关,效应和Cp , Cb 类似)
- 平行中段长度
各吃水的水线面都可有平行中段,但从上而下长度 逐渐减小。
◇中低速船的平行中段长度≈1.5~2.0Lp
- 首尾形状
首尾端形状:凸形、直线形、凹形
首端对波阻影响较大,趋势与As(x)相同
尾端涉及粘压阻力,但影响不及首端水线形状,常取直线形
- 首端进流角
水线半进角:水线在船首水平面上与船纵中剖面的夹角(不计首柱具体形状)
要考虑到水线首端形状:水线首端凸,ie大些;凹时, ie小些。
六.首尾端形状的影响
- 首端横剖面形状的影响
横剖面形状(尤其首尾附近)不仅影响阻力,而且影响推进和耐波性能。
1.1 横剖面形状的形式
通常分为U形,V形
U形特点:
① 横剖面沿吃水分布较均匀。
② 满载水线较窄,应与凹形水线配合
V形特点:
① 面积集中于中上部
② 满载水线较宽,应与凸或直线形水线配合。
1.2 横剖面形状对阻力的影响
对Rf影响小,对Rr影响大,选择时应兼顾阻力、推进和耐波性能要求。
首部横剖面形状的影响主要考虑阻力,兼顾耐波。
低速船取V形以减少Rf及舭涡。
◇中高速选U形以减少Rw(使大部分Ñ������ 分布于满载水线以下), 但不可取极端U形(避免舭涡)。
◇更高速快艇取V形,主要考虑水动力性能及耐波性。
2)尾部横剖面形状的影响
V形减阻有利,U形伴流均匀。
☆首尾端形状的选择小结:
◇ 首部:低速船用V形,中高速选U形,高速船用V形。
◇ 尾部:双桨船多用V形,单桨船多用U形。
- 首柱、尾柱形状的影响
1)垂直式船首
整个艏柱垂直形式。
优点:横剖面曲线纵向分布均匀,幅值加速度减小。
缺点:纵摇幅值大,尾倾时,艏 柱将向后倒。
目前一般不采用这种形式。
2)斜直船首
满载水线以上部分前伸,满载水线以下垂直。
优点:满载水线以上首部瘦削,前肩缓和,有利于减小纵摇和升沉运动,可增加甲板面积,船首比较美观,目前采用较多。
3)倾斜式船首
整个艏柱前倾,倾斜式船首可使满载水线以上部分的水线较为瘦削,具有减小纵摇运动、降低波浪中阻力增值、增加甲板面积、改善淹湿性和比较美观等优点。
4)球鼻艏
可减小船舶的兴波阻力、破波阻力和舭涡阻力,减阻机理与船 舶航速有关。
5)飞剪式船首
艏柱侧形呈凹形曲线向前伸出在设计水线之前,且有较大 的悬伸部。
优点:艏部体积较大而有较大的浮力储备; 艏部外飘的角度随干舷的升高而不断变大,
可避免船舶“埋首”的问题等。
6)破冰型船首
设计水线以下的艏柱侧形与基线夹角小于45°。 适用于破冰船。
- 球鼻首对阻力的影响
1) 减阻机理
① 减小兴波阻力(中高速瘦削船型)
选择适当大小和位置的球首→产生的波系与船体波系形成有利干扰→合成波↓→Rw↓。
② 减小舭涡阻力(低速肥大船,满载)埋首——船首的旋涡引起
球鼻首可使首部水流近于径向对称流动,改善首部流线→减少满载时首部舭涡→Rvp↓,埋首↓ 。
2) 球鼻艏的形式
① 水滴形
形状特点:上部小,下部大,呈水滴形。
用于船型较瘦,航速较高船舶,以减少Cw 为主。
②S-V 形
形状特点:纵剖面呈S形,横剖面呈V形。
高、中、低速,满载、压载状态下均有一定作用。 高速时产生有利干扰;低速时导流、减舭涡。
③ 撞角形
形状特点:前端较尖,呈尖角形,横剖面大致呈椭圆形。
肥大船多用,可减小舭涡、改善破波现象。
3) 球鼻的几何参数
相对突出量Lb/Lbp 相对浸深hb/T
最大宽度比bmax/B 面积比Afp/Am
相对排水体积比 d / Ñ������ ,d 球鼻的排水体积
- 特殊船尾形状
4.1 方尾
常规船型,大多数船舶采用巡洋舰型船尾。
优点:满载水线附近的尾部水线向后作适当延长,水线长度↑,Rw↓Rvp↓;
尾部甲板面积↑,初稳性↑,便于布置舵机,同时对螺 旋桨和舵有保护作用,可提高推进效率。
缺点:构造复杂且后垂线处船体应力将加大,限制螺旋桨直
方尾船型水动力特点:
低速时,方尾尾部水流不能沿着船体的底部和两侧向后迅 速脱离开船体,所以在尾后形成大量的旋涡,对阻力不利。
•�������� Fr>0.4时,船尾部的水流具有足够的动能以克服粘性的影 响迅速脱离开船的尾部(这种现象称为水流突离现象)。
•�������� 方尾的后部不再出现旋涡,而是船侧和尾底的水流在船后 的某个位置交汇,形成鸡尾状的水丘。在水丘与尾板之间形成“空穴”
方尾的优点:
尾部纵剖线平直(坡度缓和近于直线)
→高速时水流基本沿纵剖线方向流动
→减能耗(减少水流的扭转和弯曲程度)→降阻力。
高速水流沿着方尾边缘一直向后延伸→尾部形成空穴
→船体有效长度↑→Rr↓但Rf 不增。(∵湿面积未增)
“虚长度作用”:高速水流沿着方尾边缘一直延伸到尾后相 当距离处,其作用相当于增加了船体的有效长度,从而有利于减小Rr。
尾部排水体积大,可减小尾倾,改善“ 鸡尾流” 现象。
结构简单,较好的回转性,对螺旋桨等有良好的保护作用。
4.2 球鼻形船尾(比球首研究得少)
V形,U形,球尾形——三种尾型的比较:
V形阻力性能好,但推进性能差。
U形螺旋桨伴流均匀,推进性能好,但阻力较V形差。
球尾综合性能最佳。
4.3 双尾和双尾鳍
浅吃水或超浅吃水船一般采用双桨船型,但其推进 斜率较低且附体阻力较大→ 开发双尾和双尾鳍船型
(1) 双尾
•�������� 两个单体船艉联起来,中间平坦过渡。
•�������� 推进性能较一般双桨船好,伴流好,船身效率高。
•�������� 阻力性能不差(纵向梯度↓片体薄→ Rvp↓、Rw↓,Rf↑但附体 阻力显著↓ )。
•�������� 与双桨船相比,桨在船尾中央,伴流均匀,阻力和推进一起 得利。
(2) 双尾鳍
•�������� 不用轴包架,在轴包架基础上发展成双尾鳍,把它变成为船 型的一部分 → 推进性能更↑。
•�������� 双尾鳍较适合海上航行,不用担心螺旋桨出水;双尾船不适 合海上航行,尾部砰击大,螺旋桨受影响。
4.4 涡尾及不对称船尾
机理: (实为变形尾鳍)形成一股与螺旋桨旋向相反的旋转 水流,改善螺旋桨的周向诱导速度,提高推进性能。
◇ 不对称船尾:用于单桨船。
◇ 涡尾:用于内河双桨船。
4.5 隧道形船尾
内河船,受吃水限制,为了增大螺旋桨直径而采用。
◇ 闭式,阻力大,但倒车性能较好。
◇ 为了保证螺旋桨充足供水,以开敞式为佳。
- 纵流船型
为适应内河船舶T小B大的特点而开发。
常规船型船首散波较大。
纵流船型,横剖面近于长方形,有压浪作用。
周围流动与性能特征:
大部分水流沿纵剖线直线流向船底→梯度小→R↓
沿船体流动的水流大部分被船体所“覆盖”→ 压浪,且水 线面大、稳性↑
优点:降阻、消波、稳性好。
缺点:风浪中拍击现象严重,总纵强度、抗弯抗扭刚度差。
第十三章 阻力的近似估算方法
确定船舶阻力最准确的方法是通过船模试验,这也是目前应用最为广泛的方法。
但在船舶设计初期(如方案设计阶段),船舶的主尺度和船型系数已经确定,但型线尚未确定,此时还不能通过模型试验方法确定船模阻力,只能用近似方法对船舶阻力进行估算。
阻力估算的目的:
1)在主机已定的情况下,预报船舶能够达到的最大航速;
2)在设计航速已知的条件下,确定船舶所需的主机功率。
一.近似估算方法分类
1、按照计算内容划分:
1)直接近似估算总阻力或有效功率;
2)先估算剩余阻力,再根据相当平板公式计算摩擦阻力。
2、按照估算所采用资料的形式划分:
1)图谱法; 2)回归公式法。
3、按照估算所采用资料的来源划分:
1)母型船数据估算法;
2)应用模型系列试验资料估算法;
3)归纳模型和实船资料分析估算法。
在实际船舶设计中,应根据设计船与母型船或设计船与阻力估算图谱所依据的船模系列之间的相似程度等多方面因素,有针对性地选择估算方法,来提高阻力估算的准确程度。
二.模型系列试验图谱估算法
应用模型系列试验图谱估算法就是根据模型系列试验资料,直接给出阻力图表,在此图表的基础上对设计船的阻力进行估算。在实际使用过程中,应针对设计船泊的类型,选择相应的模型系列试验图谱进行估算。
常用的模型系列试验图谱包括:泰洛(Taylor)系列图谱、系列60图谱(又称陶德(Todd)系列)、瑞典的SSPA系列图谱、英国的BSRA运输船系列图谱等,本书中重点介绍泰勒系列图谱和系列60图谱,其他图谱可参照相应手册。
(一)泰洛系列图谱估算法
该系列图谱的母型船是一艘双桨、U型横剖面的巡洋舰,故该系列模型试验图谱可用于军舰的阻力估算,也可用于民用双桨船阻力估算。
•�������� 早期的泰洛系列试验图谱:单位排水量剩余阻力等值线的形式,英制单位。
•�������� 1954年盖特勒对泰洛标准阻力数据进行了重新分析整理:
无量纲的剩余阻力系数图表(不同排水体积系数(∨/L3),Cr—V/L0.5关系曲线)——设计船的剩余阻力系数;
无量纲的湿表面积系数图谱——船体湿表面积,并记入一定的粗糙度补贴,桑海公式——摩擦阻力系数。该系列图谱亦称为泰洛-盖特勒系列图谱。
- 图谱形式和参数范围
给出的图谱形式为:对每一组B/T,以每一棱形系数Cp给出一张图谱,图中以不同排水体积系数为参数,作出剩余阻力系数Cr对Fr(或V/L0.5)的关系曲线。
2.无量纲湿面积系数Cs图谱
Cs图谱的形式为,以每一组B/T值给出一张图谱,表示为在不同Cp和 ![]() 时的Cs等值曲线。显然,根据设计船的B/T,Cp和
时的Cs等值曲线。显然,根据设计船的B/T,Cp和 ![]() 值,由该图谱可查得Cs值,进而可按下式求得船体的湿面积。
值,由该图谱可查得Cs值,进而可按下式求得船体的湿面积。
3. 适用的参数范围
(二)泰洛法阻力估算的具体步骤
a、计算设计船的船型参数B/T、Cp、▽/L3和Fr。
b、求湿面积系数Cs。
有型线图 — 计算S`— 计算Cs `= S ` /( ▽L )0.5
无型线图 — 查Cs图谱 — 插值计算得Cs
如无型线图,则可近似认为其湿面积与标准船型湿面积相等,则可按照给定的B/T值选用与其最接近的两张Cs图谱,并由给定的Cp、▽/L3值查得Cs值,然后对B/T进行线性内插。
c、计算摩擦阻力系数Cf值。
桑海 Cf=0.4631/(lgRe)2.6 △Cf=0.4*10-3
注意:计算雷诺数时的船长应取水线长度。
d、求剩余阻力系数Cr值。
由B/T,Cp,▽/L3 、Fr选Cr 图谱 — 内插得Cr
如实船Cs ,与标准船Cs不同,Cr须修正
Cr `=Cr*Cs/Cs `
e、计算总阻力Rt、有效功率Pe值。
总阻力系数:Cts=Cr`+Cf+ △Cf
总阻力 : Rts=Cts*0.5��������v 2S` (N)
有效功率:Pe=Rts v/1000 (kw)
不同V—重复上述计算—v-Pe曲线
母型—巡洋舰
—适用航速较高船型较瘦(双桨)
—普通货船结果偏低
(三)系列60图谱法
系列60图谱:是由系列60船模阻力试验结果绘制成的,对每一组B/T,针对每一个Fr有一幅图谱。
- 系列60图谱法
作为标准船型的系列60在民用船舶中应用较广泛,适用于估算单螺旋桨运输船的阻力。其以一组不同方形系数母型船模为基础,首先系列地变化其浮心纵向位置,然后对不同方形系数的母型船保持其浮心在最佳纵向位置不变,系统地变化L/B、B/T而形成的。
采用系列60图谱对设计船进行阻力估算时,剩余阻力采用图谱进行计算,摩擦阻力采用桑海公式进行计算,并计入一定的粗糙度补贴系数△Cf=0.2~0.4×10-3。
船体湿表面积可由型线图计算求得,亦可由三种B/T状态下的该系列湿表面积 系数图谱查得。
三.经验公式估算法
(一) 艾亚(Ayre)法(爱尔法)
适用:中、低速商船(包括正常尺度的海洋拖轮)
单位:公制有效功率
包含单桨货船常规附体、空气阻力(约占Rt 8%)
对双桨船阻力和上层建筑过大者需另行修正
船型比较老,近代肥大型船舶误差大
1、艾亚法基本思想
标准船型—有效功率;
设计船—标准船—比较—逐项修正
(二) Lap-Keller法
此法将剩余阻力和摩擦阻力分开进行计算,是根据图谱。
摩擦阻力根据桑海公式计算。△Cf由表2-3选取。
确定剩余阻力的方法
① 根据Cp和xc由图7-5确定该船属于哪组。
如果Cp>0.8且L/B≠6.5,进行修正。
② 计算Cr—Rr——Rt
③ B/T≠2.4 修正
△Rt=±10(B/T-2.4)×0.5%Rt
2.4<B/T<3.0 取正;其他取负。 总阻力=Rt+ △Rt
四.母型船数据估算法
母型船数据估算法具有简单、方便的特点,在方案设计阶段可以实现快速确定设计船的阻力或有效功率。但采用该方法估算结果的准确性取决于设计船与母型船的相似程度和母型船数据的可靠性。
常用的母型船数据估算法:
- 海军部系数法
- 引伸比较定律法
- 基尔斯修正母型船剩余阻力法
(一) 海 军 部 系 数 法
海军部系数法是母型船数据估算法中最常用的一种估算方法,基础是假定设计船与母型船在傅汝德数相等时,两者的海军系数相等。
1)当设计船与母型船船型的佛汝德数相近时,可近似认为两船的剩余阻力系数Cr相等;
2)当设计船与母型船船型、主尺度和雷诺数相近时,可近似认为两船的摩擦阻力系数Cf相等;
3)当设计船与母型船船型的主尺度相近时,可近似认为两船的湿表面积S与排水量△的2/3次方成比例。
海军系数Ce反映的是船舶的阻力性能,当我们用主机功率Pm替换有效功率Pe,则海军系数可表达为:
式子中的海军系数Cm反映了船舶的快速性能,其中包含了阻力和推进两方面的内容。当主机功率P给定时,海军部系数Cm越大,则其快速性越好。
可见,对应不同的功率,将有不同含义的海军系数。
船舶设计中,当有相近的母型船数据时,应用海军部系数法可以方便地在给定船舶排水量和主机功率条件下估算设计船所能达到的航速;或在给定排水量和航速要求条件下估算设计船所需主机功率。
(二) 引伸比较定律法
在船舶设计中,当有相近的母型船资料时,应用引申比较定律法可以在给定船舶排水量时,利用母型船的功率-航速关系曲线,计算出设计船在航速U2时的母型船相应航速V1=V2(△1/△2)1/6,然后在母型船的功率-航速关系曲线上查得V1所对应的功率P1,则设计船在V2时的功率P2=P1(△2/△1)7/6。
(三) 基尔斯修正母型船剩余阻力法
前面两种船舶阻力估算方法,均是在设计船与母型船相似的条件下,当两船的佛汝德数相等时,利用其剩余阻力系数相等而完成的阻力近似估算。
当设计船与母型船不相似,或相似程度较低时,即使在相同的Fr下,其剩余阻力系数也不相同,此时可以采用对母型船的剩余阻力系数进行修正的方法,得到设计船的剩余阻力系数,再按照相当平板摩擦阻力计算公式计算得到其摩擦阻力系数,完成对设计船的总阻力或有效功率的估算。
其中比较有代表性的是基尔斯修正母型船剩余阻力法。
1