第四章 动能和势能
教学时数:11
教学目的与要求:
（1）着重讲授正功与负功的意义，变力的功以弹性力的功为主，可用图解法导出其计算公式。
（2）关于系统的势能，本章仅讲授重力势能及弹性势能。
（3）使学生深刻地认识功能关系，并指出功是能量变化的量度，能是以作功的方式传递并转化的。
（4）结合本章内容，指出只有量纲相同的物理量间才能构成等式关系。
（5）分别讲授质点的与质点组的功能原理与机械能守恒定律，并通过势能曲线研究动能与势能间的相互转化关系。
（6）讲授质点组的功能原理时，要阐明内力做功与内势能的概念。
（7）要分清动量守恒定律与现机械能守恒定律的适用条件的不同，使学生能正确运用两个守恒定律解决实际问题。
教学重点:
功，变力的功；功率，动能，动能定理；保守力与非保守力；势能（重力势能、弹性势能、引力势能）势能曲线和从势函数求力；功能原理；力学中的能量守恒定律；普遍的能量转换和守恒定律, 对心和非对心碰撞
教学难点:
动能定理; 功能原理; 能量守恒定律
本章主要阅读文献资料:
顾建中编 《力学教程》 人民教育出版社
赵景员、王淑贤编 《力学》 人民教育出版社
漆安慎 杜婵英 《〈力学基础〉学习指导》 高等教育出版社
能量——另一个守恒量
能量概念的认识和由来:
从“使物体运动起来需要付出代价”（人们最早对生活中实际的问题的认识）；
“运动的物体具有某种功效（例如：运动的子弹可以嵌入泥土）”；
1686年莱布尼茨提出：物体“运动的量”与物体速度平方成反比；
1965年,“运动的量”发展为“
”,并称作“活力”；科里奥利称之为“功”；
1801年，托马斯·杨提出将“ ”称作“能”，“功能原理”和“机械能守恒”思想，
自然界一切过程都必须满足能量守恒定律；
从经典物理学到现代物理学，对能量的认识发生了巨大的变化：
能量可连续取值 
普朗克指出：物体只能以
为单位发射和吸收电磁波 微观世界的原子光谱是线状谱 能级是分立的。
可以看出：能量概念最早源于生产 经过概念的比较和辨别 升华为科学的概念。
力的元功
我们知道：自然界中能量是守恒的，但能量还是可以转移和改变形式的，而改变能量的手段就是做功。
一. 力的元功和功率
在以前学过：功是力在受力质点的位移上的投影与位移的乘积。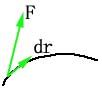
其成立的条件：力是恒力且质点沿直线运动。
对于力是一变力，且质点沿曲线运动的一般情况：
方法：将物体的位移“细分”成许多小段，每段可视为方向不变的小位移，小位移上的力可认为是不变的。
元位移：无穷小的位移，可以认为合轨迹重合。
1. 元功：力在元位移上的功称为元功——标量。
力的元功等于力
与受力质点无穷小位移 
的标积：
(1)
表示力与位移的夹角：
正功；
0；
负功。
注意：（1）功的位移指受力点的位移，若为质点，就是质点的位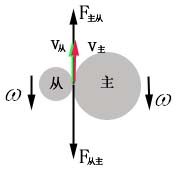
移
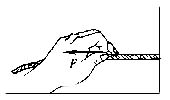
例如：手握住一端固定于墙壁的绳并在绳上滑动，绳上的受力点不断变化，但受力并未发生位移，故作用于绳上的摩擦力不做功。但绳子对手的摩擦力做功。
例如：人在路面上行走时，
不做功，因为有力时，没有位移；有位移时没有力。
常用判别式：
受力点不断转移时，应用此事来判断， 
为受力物体受力点相对于计算功参照系的速度。
例：齿轮的转动：主动轮对从动轮做正功，从动轮对主动轮做负功
（2）功和参考系有关。（因为：位移和参考系有关系）
例：一辆汽车以
运动，突然急刹车，最后静止，求摩擦力所作的功。
， 
， 
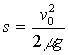
摩擦力相对于地面的功为：
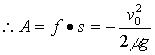(2)
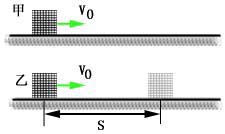
上述同样的车和另一辆并排的甲车以
作匀速直线运动， 
为乙车相对甲车的位移。
， 
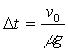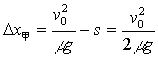
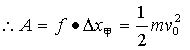(3)
(2)式表明：以甲车为参考系，
做正功。
因此，由于位移
和参考系有关，故摩擦力做负功的说法为错。
与此相联系：机械能守恒定律与参考系也有关，在一个惯性系中守恒，但在另一惯性系中就不守恒。
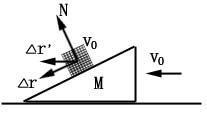
例如：斜面上的物体
沿光滑的斜面下滑， 
相对于地面以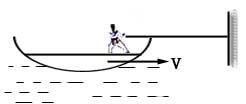 
向左方运动，不计摩擦力。
以斜面为参考系，物块 机械能守恒， 
；
以地面为参考系，物块 机械能不守恒， 
。
另外：关于位移 的解释还可举例如下：
同样，绳子对人的拉力做功，但人对绳子的拉力不做功，因为人对绳子施力，但作用点的绳子没有位移。
2．若多个力
作用于质点，位移 ，则合力的功为：
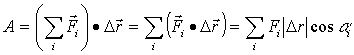
即 ：合力所做的功等于分力所做功的代数和。
3．平均功率：
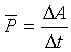
即：功与时间的比值叫做该段时间的平均功率：平均做功的快慢
4． 瞬时功率：当时间
趋于零时，力的平均功率的极限叫力的瞬时功率。
数学公式：
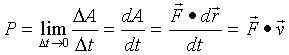(4)
即：力的功率等于力与受力点速度的标积。
二. 不同坐标系元功的表示
1.平面直角坐标系
力：
元位移：
元功：
(5)
例：若质点做直线运动，令
轴和位移重合，则：
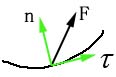2.平面自然坐标系
力：
；元位移： 
元功：
(6)
即：功等于力在切向单位矢量上的投影和弧坐标增量的乘积。
3.极坐标系
力：
； 元位移： 
元功：
(7)
一般说来，常用的形式是：直角坐标系形式和自然坐标系形式 。
方法：用积分描述受力质点在有限路径上的功。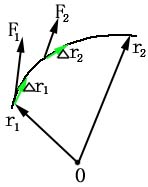
讨论：力 自 
沿曲线至 
做的功：
“细分”：位移看作由许多元位移 
组成，
力的元功：
“做和”：总功：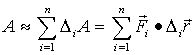 
“求极限”：元位移的数目n无限增多，而
，则上式和式的极限给出功的精确值。
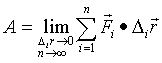
该和式的极限称作力 沿曲线自 至 的线积分，记作：
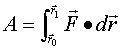(8)
(8)式表明：变力的功等于元功之和。
注：(8)式的线积分除与力 有关外，还与积分路径有关。
例：在直角坐标系中：
自然坐标系中：
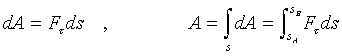
平面极坐标系中：
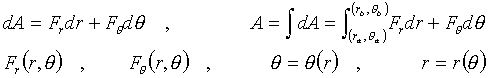
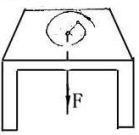
练习题：如图，一轻细线系一小球，小球在光滑水平桌面上沿螺旋线运动，绳穿过桌中心光滑圆孔，用力F向下拉绳。证明力F对线作的功等于线作用于小球的拉力所作的功，线不可伸长。
质点和质点系动能定理
一. 质点的动能定理：
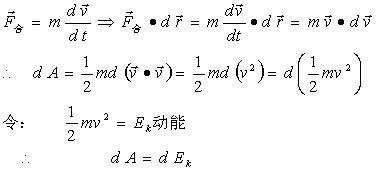(1)
(1)式表明：合外力所做的元功等于动能的微分。
例：在自然坐标系中，
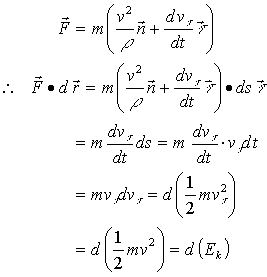
即：质点动能的微分等于作用于质点的合力所做的元功—— 质点的动能定理的积分形式：
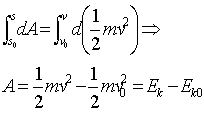(2)
(2)式表明：质点动能的增量等于作用于质点的合力所做的功, 对应于非无限小的过程。
注：功描述的是：力对空间积累的效果，是一过程量；而动能与质点运动的速度有关，是一状态量。
二．质点系内力的功
如图示：两质点沿虚线轨迹运动，相对于参考点O的位置矢量各为
和 
， 
表示质点1对2的作用力， 
表示质点2对1的作用力， 
，这对作用力元功之和为：
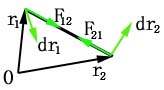
令：
，是质点2相对于质点1的位矢，则：
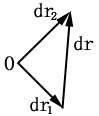设：
的单位矢量是 
，则：
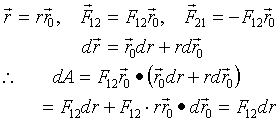(3)
即：二质点间相互作用力所做的元功的代数和等于作用于其中一质点的力与该质点相对于另一质点元位移的标积。
也即：二质点间作用力和反作用力所做功的代数和决定于力和质点间相对距离的改变。
三. 质点系的动能定理
设：质点系有几个质点，作用于各质点合力的功等于
各质点的初始动能和末动能分别是：
和 
由：质点的动能定理得：
上式对于一切质点取和：
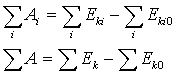(4)
定义：质点系的动能：质点系内各质点动能之和。
将(4) 中的功分为两部分：
,故：
(5)
即：质点系动能的增量等于一切外力所做功与一切内力所做功的代数和，称作质点系的动能定理。
注：内力功的推论：
① 若二质点间的距离不变
，则它们之间的内力功为零。
② 刚体的内力功为零。
练习题：轻且不可伸长的线悬挂质量为500g的圆柱体。圆柱体又套在可沿水平方向移动的框架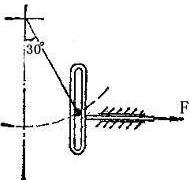
内，框架槽沿铅直方向。框架质量为200g。自悬线静止于铅直位置开始，框架在水平力F=20.0N作用下移至图中位置，求圆柱体的速度。线长20cm。不计摩擦。
保守力与非保守力 势能
一. 力场
场力定义：质点所受的力仅与质点的位置有关。
例如：重力：
重力场 弹簧的弹性力场 
电磁力场和引力场 
洛伦兹力
和摩擦力 
均不是力场。
有心力：质点所受力的作用线总通过一点，则该力称有心力。
例如：总电荷的电场是一有心力场。弹簧的弹性力场是有心力场。
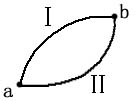二.保守力与非保守力
1. 保守力
定义：力所作的功与路径无关，仅由质点的始末位置决定。
如图示：
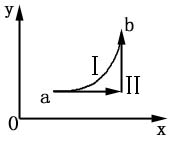
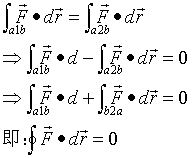
即：保守力沿闭和路径所做的功为零。
2. 非保守力
定义：力所做的功不仅决定于受力质点的始末位置，而且和质点经过的路径有关；或：力沿闭和路径所做的功不等于零。
例如：摩擦力。
力学中常见的保守力
a.重力：
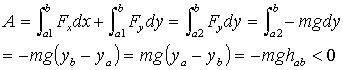
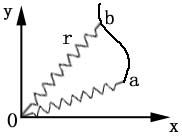b.弹性力：
设：弹簧原长是
,在图中任一位置 
处（ 
是 方向的单位矢量）：
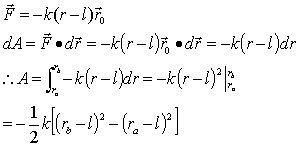
用
表示形变量，有：
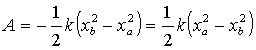
c.万有引力：
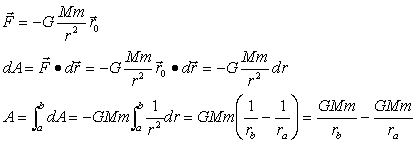
由此可见：静电库仑力也是保守力。
三.势能
设质点由 位置 
到达 位置 
重力的功：
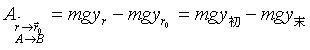
弹性力的功：
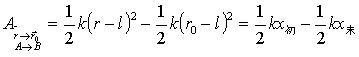
万有引力的功：
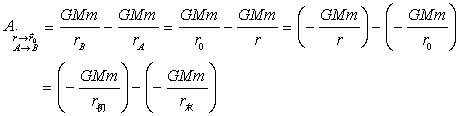
（以前谈到“增加”，指：末减初；若是初减末，则为“减少量”）
由上面的例子可知：质点在保守力场中运动，保守力所做的功是（对应于）质点的位置的某个函数
的减少量。这个函数就叫势能函数，用 
表示。
由此可见：保守力做正功，势能减少
，即： 
或者：保守力所做的功的负值，对应于势能的增加。即：
由上述讨论可知：重力势能函数：
弹性势能： 
万有引力势能：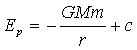
c是由势能零点来决定的。
若：对于重力势能：
弹性势能：
万有引力势能：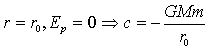
势能和保守力是相对应的。势能值不是绝对的，而是相对的，依据于势能零点的选取。
若选择保守力做功的起始为势能零点，则终止位置的势能为：
即：一定位置的势能在数值等于从势能零点到此位置保守力所做功的负值。
或：一定位置的势能等于从该位置到势能零点保守力所做的功。即：
， 
例如： 
表明： 
；
表明： 
；
表明： 
。
由此可见：不能说，万有引力势能总是负的，而与势能零点的选取有关。
总结：保守力和势能的关系：
①：保守力和势能相对应；反之亦然。
②：保守力所做的功等于势能的减少量：
， 
③：保守力场中任一点的势能，等于从该点到势能零点保守力作的功。
， 
④：保守力场中任一点的势能值是相对的，不是绝对的，依据于势能零点的选择，势能函数间相差一常数，保守力场中某二点之间势能的变化是绝对的，不依据于势能零点的选择。
⑤：保守力的方向与等势面垂直，指向势能减少的方向。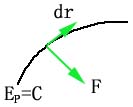
∵ 沿等势面，保守力不做功，
∴ 
又有：
， 
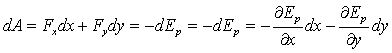
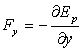
若：对于三维情况：
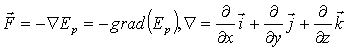
可见：
例：如图示，一根弹簧，在O点时，是自由伸展的，由
的过程外力做功1J，求：A，B，C，D点的势能。（各段间距离是相等的，且为1个单位）
解：若取O点为势能零点，则：
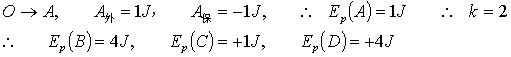
若取A点为势能零点，则：
当 
又 
四． 势能是物体相对位置的函数
因势能与保守力相联系，故势能是属于以保守力相互作用的，是系统所共有的，不是一个物体所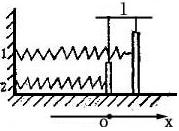
具有的。
练习题：二仅可压缩的弹簧组成一可变刚度系数的弹簧组，弹簧1和2的刚度系数各为k1和k2。它们自由伸展的长度相差L。坐标原点置于弹簧2自由伸展处。求弹簧组在
和x<0时弹性势能的表示式。
功能原理和机械能守恒定律
一. 质点系的功能原理：
由质点系的动能定理可得：
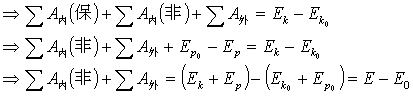
即：
(1)
即：质点系机械能的增量等于一切外力和一切内非保守力所做功的和，称作质点系的功能原理。
由此可见：①只有外力和内非保守力才会引起机械能的改变。
②内保守力做功所引起的作用是：会引起质点系动能的改变，但不会引起质点系机械能的改变。
注意：在应用“功能原理”时，若左方计入保守力的功，则右方就不再考虑对应的势能。
在应用“功能原理”时，若右方计入势能，则左方就不再考虑对应的保守力的功。
二.机械能守恒定律
由(1)式可知：若体系所受的外力功为零，内非保守力做功为零，则机械能守恒。
若： 
(2)
若：体系仅有内保守力做功，则机械能守恒。
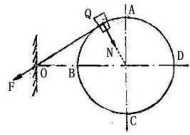练习题：物体Q与一刚度系数为24N/m的橡皮筋连接，并在一水平圆环轨道上运动，物体Q在A处的速度为1.0m/s，已知圆环的半径为0.24m，物体Q的质量为5kg，由橡皮筋固定端至B为0.16m，恰等于橡皮筋的自由长度。求（1）物体Q的最大速度； （2）物体Q能否到达D点，并求出在此点的速度。
对心碰撞
一. 碰撞的特点和简化处理：
①碰撞时间短，相互作用强，可不考虑外界的影响；
②碰撞前后状态变化突然且明显，可以认为：速度发生变化，但位置不发生变化。
二.对心碰撞：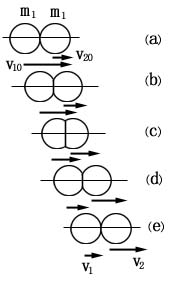
1.对心碰撞：碰撞前后的速度都沿两球的连心线，也叫一维碰撞。
2.碰撞过程：
①压缩过程：从两小球开始接触到两小球达到共同速度。（b）和（c）图，特点：
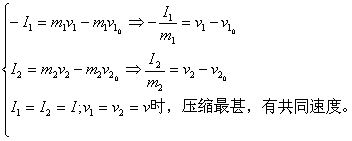
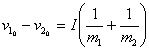
②恢复过程：从共同速度到分离的过程。（d）（e）图，特点：
（恢复冲量）
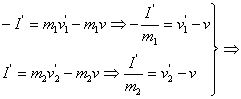
消去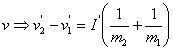 
称：
为接近速度， 
为分离速度。
3.牛顿碰撞公式：
实验表明：对于材料一定的球，碰撞后分开的相对速度与碰撞前接近的相对速度成正比，比值称为恢复系数：
（ 
）
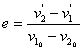4．完全非弹性碰撞（
）
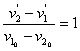
动量守恒：
(1)
机械能守恒：
(2)
(2)
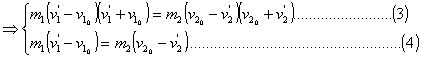
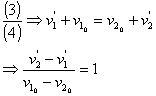
所以：可以联上三式中任意二式，不妨：
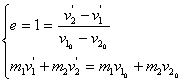
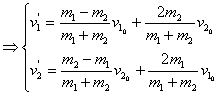
当
时： 
当
，且 
时： 
当
，且 时： 
5． 完全非弹性碰撞：
动量守恒定律：
损失的动能：
6． 非完全弹性碰撞：
动量守恒定律：
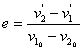
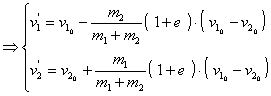
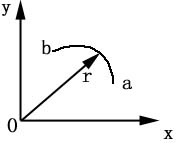
7．非对心碰撞：
定义：如果两球相碰之前的速度不沿它们的中心连线，叫非对心碰撞，也叫斜碰。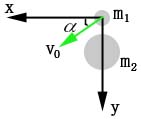
设二球的质量： 
和 
， 
即： 静止。设球表面光滑，相碰时二球相互作用力沿二球接触时连心线方向，如图示 
与x轴的夹角为 
，则：
x方向：
y方向：对心碰撞：
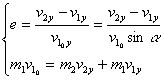
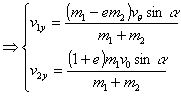
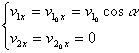
若：
，即小球与光滑的无穷大的平面相碰，可知：
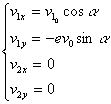
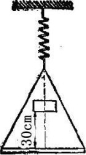1.一质量为200g的框架，用一弹簧悬挂起来，使弹簧伸长10cm，今有一质量为200g的铅块在高30cm处从静止开始落进框架。求此框架向下移动的最大距离。弹簧质量不计，空气阻力不计。
2.质量为m1=0.790kg和m2= 0.800 kg 的物体以刚度系数为 10N/m 的轻弹簧相连，置于光滑水平桌面上。最初弹簧自由伸张、质量为 0.01kg 的子弹以速度 v =100m/s 沿水平方向射于m1
内，问弹簧最多压缩了多少？
本章要点:
功，变力的功；功率，动能，动能定理；保守力与非保守力；势能（重力势能、弹性势能、引力势能）势能曲线和从势函数求力；功能原理；力学中的能量守恒定律；普遍的能量转换和守恒定律, 对心和非对心碰撞
本章习题: 4.2.5, 4.3.3, 4.5.1, 4.5.2, 4.6.5, 4.6.6, 4.6.10
1